
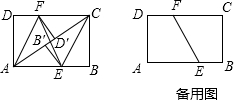
分析 (1)由折叠的性质得出∠DAF=∠CAF=$\frac{1}{2}$∠DAC,∠BCE=∠ACE=$\frac{1}{2}$∠ACB,B′C=BC,∠CB′E=∠B,由矩形的性质得出∠D=∠B=90°,AB=DC=4,BC=AD=3,AD∥BC,证出∠DAF=∠BCE,由ASA证明△ADF≌△CBE即可;
(2)由勾股定理求出AC,得出AB′=2,设BE=x,则B′E=x,AE=4-x,由勾股定理得出方程,解方程求出BE,设EF交AC于O,则OE=OF,OA=OC=$\frac{1}{2}$AC,求出OB′,由勾股定理求出OE,即可得出EF的长;
(3)分三种情况:①当CM=CN时,设FN=x,则CM=CN=x+$\frac{5}{2}$,BM=x+$\frac{3}{2}$,在Rt△BCM中,由勾股定理得出方程,解方程得出PN,不合题意舍去;
②当MC=MN=EF=$\sqrt{10}$时,在Rt△BCM中,由勾股定理求出BM,得出CN=2BM=2,即可得出结果;
③当CN=MN=$\sqrt{10}$时,得出ME=NF=$\sqrt{10}$-$\frac{5}{2}$,求出BM,由勾股定理求出MC2,即可得出结果.
解答 (1)证明:由折叠的性质得:∠DAF=∠CAF=$\frac{1}{2}$∠DAC,∠BCE=∠ACE=$\frac{1}{2}$∠ACB,B′C=BC,∠CB′E=∠B,
∵四边形ABCD是矩形,
∴∠D=∠B=90°,AB=DC=4,BC=AD=3,AD∥BC,
∴∠DAC=∠ACB,
∴∠DAF=∠BCE,
在△ADF和△CBE中,$\left\{\begin{array}{l}{∠D=∠B}\\{AD=BC}\\{∠DAF=∠BCE}\end{array}\right.$,
∴△ADF≌△CBE(ASA);
(2)解:∵∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴AB′=AC-B′C=AC-BC=5-3=2,
设BE=x,则B′E=x,AE=4-x,
∵∠AB′E=180°-∠CB′E=180°-∠B=180°-90°=90°,
∴AB′2+B′E2=AE2,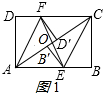
即22+x2=(4-x)2,
解得:x=$\frac{3}{2}$,
即BE=$\frac{3}{2}$,
设EF交AC于O,如图1所示:
则OE=OF,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×5=$\frac{5}{2}$,
∴OB′=$\frac{5}{2}$-2=$\frac{1}{2}$,
∴OE=$\sqrt{(\frac{3}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{10}}{2}$,
∴EF=2OE=$\sqrt{10}$;
(3)解:分三种情况:①当CM=CN时,如图2所示: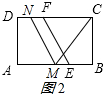
由(2)得:BE=$\frac{3}{2}$,CF=AE=4-$\frac{3}{2}$=$\frac{5}{2}$,
设FN=x,则CM=CN=x+$\frac{5}{2}$,BM=x+$\frac{3}{2}$,
在Rt△BCM中,由勾股定理得:BC2+BE2=MC2,
即32+(x+$\frac{3}{2}$)2=(x+$\frac{5}{2}$)2,
解得:x=$\frac{5}{2}$(不合题意,舍去);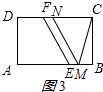
②当MC=MN=EF=$\sqrt{10}$时,如图3所示:
在Rt△BCM中,BM=$\sqrt{M{C}^{2}-B{C}^{2}}$=$\sqrt{10-{3}^{2}}$=1,
∴CN=2BM=2,
∴MC2+MN2+CN2=($\sqrt{10}$)2+($\sqrt{10}$)2+22=24;
③当CN=MN=$\sqrt{10}$时,如图4所示: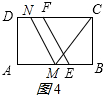
ME=NF=$\sqrt{10}$-$\frac{5}{2}$,
∴BM=$\sqrt{10}$-$\frac{5}{2}$+$\frac{3}{2}$=$\sqrt{10}$-1,
∴MC2=BC2+BM2=32+($\sqrt{10}$-1)2=9+11-2$\sqrt{10}$=20-2$\sqrt{10}$,
∴MC2+MN2+CN=20-2$\sqrt{10}$+10+10=40-2$\sqrt{10}$.
点评 本题是四边形综合题目,考查了矩形的性质、勾股定理、全等三角形的判定与性质、等腰三角形的性质等知识;本题综合性强,难度较大,特别是(3)中,需要进行分类讨论才能得出结果.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:选择题
| A. | a2+b2=(a+b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3 | D. | a2-2ab+b2=(a-b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
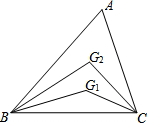 已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,
已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
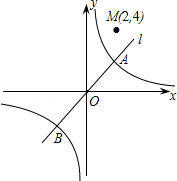 通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=$\frac{k}{x+2}$(k≠0)的图象是由反比例函数y=$\frac{k}{x}$(k≠0)的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.如图,已知反比例函数 y=$\frac{4}{x}$的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=$\frac{k}{x+2}$(k≠0)的图象是由反比例函数y=$\frac{k}{x}$(k≠0)的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.如图,已知反比例函数 y=$\frac{4}{x}$的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
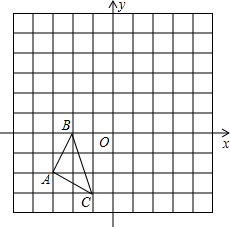 如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.
如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com