
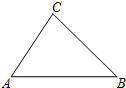
 如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值.
如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值. 分析 首先过点C作CD⊥AB,垂足为D,解Rt△CDB,求出CD=BD=2,再解Rt△ACD,求出AD=$\frac{2\sqrt{3}}{3}$,那么AB=AD+BD=$\frac{2\sqrt{3}}{3}$+2,然后根据S△ABC=$\frac{1}{2}$AB•CD,计算即可求解.
解答 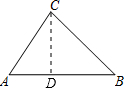 解:过C作CD⊥AB,垂足为D.
解:过C作CD⊥AB,垂足为D.
在Rt△CDB中,sin∠B=$\frac{CD}{BC}$,cos∠B=$\frac{BD}{BC}$.
∵∠B=45°,BC=$2\sqrt{2}$,
∴$CD=2\sqrt{2}×sin{45°}=2\sqrt{2}×\frac{{\sqrt{2}}}{2}=2$,$BD=2\sqrt{2}×cos{45°}=2\sqrt{2}×\frac{{\sqrt{2}}}{2}=2$.
在Rt△ACD中,cot∠A=$\frac{AD}{CD}$.
∵∠A=60°,CD=2,
∴$AD=2×cot{60°}=2×\frac{{\sqrt{3}}}{3}=\frac{2}{3}\sqrt{3}$,
∴$AB=AD+BD=\frac{2}{3}\sqrt{3}+2$,
∴${S_{△ABC}}=\frac{1}{2}×(\frac{2}{3}\sqrt{3}+2)×2=\frac{2}{3}\sqrt{3}+2$.
点评 此题考查了解直角三角形,三角形的面积,熟练应用锐角三角函数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a2+b2=(a+b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3 | D. | a2-2ab+b2=(a-b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
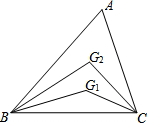 已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,
已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
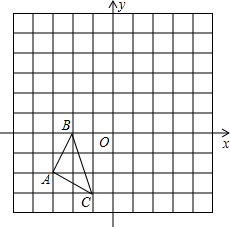 如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.
如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com