
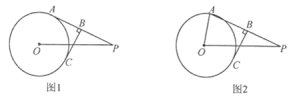
【题目】已知点A是⊙O上一点,P是⊙O外一点,AP的垂直平分线与⊙O相切于点C,交AP于B点.
⑴ 如图1,若PA是⊙O的切线,求![]() 的值;
的值;
⑵ 如图2,若PA与⊙O相交,OA=4,OP=10,求AP的长.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)连接OA、OC,先证明四边形OABC是正方形,从而得出OA=AB=BP,设OA=x,则AP=2x,在Rt△OAP中OP=![]() ,再求其比值;
,再求其比值;
(2)作OE⊥AP于E,连OC,先证明四边形OABC是正方形,从而得出OE=EB=OA, 设AB=BP=x,则AE=AB-BE=x-4,根据OA2-![]() =OE2=OP2-PE2列出方程,解方程,从而求出AP的长.
=OE2=OP2-PE2列出方程,解方程,从而求出AP的长.
(1)连接OA、OC,如图所示:

∵若PA是⊙O的切线,AP的垂直平分线与⊙O相切于点C
∴∠OAB=∠ABC=∠OCB=90o,AB=PB,
∴四边形OABC是矩形,
又∵OA=OC,
∴四边形OABC是正方形,
∴OA=AB,
∴OA=AB=BP
设OA=x,则AP=2x,在Rt△OAP中OP=![]() ,
,
∴![]() ;
;
(2)作OE⊥AP于E,连OC,

∵若PA是⊙O的切线,AP的垂直平分线与⊙O相切于点C
∴∠OEB=∠EBC=∠OCB=90o,AB=PB,
∴四边形OEBC是矩形,
又∵OE=OC,
∴四边形OEBC是正方形,
∴OE=EB,
∴OE=EB=OA,
设AB=BP=x,
则AE=AB-BE=x-4,∵OA2-![]() =OE2=OP2-PE2,
=OE2=OP2-PE2,
∴42-(x-4)2=102-(x+4)2,
∴x=![]() ,
,
∴AP=2x=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的题目及分析过程.已知:如图点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]()



原图 ① ②
说明:![]()
说明两个角相等,常用的方法是应用全等三角形或等腰三角形的性质.观察本题中说明的两个角,它们既不在同一个三角形中,而且们所在两个三角形也不全等.因此,要说明![]() ,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
如图①过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
如图②延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请从以上两种辅助线中选择一种完成上题的说理过程.
(2)在解决上述问题的过程中,你用到了哪种数学思想?请写出一个._______________.
(3)反思应用:

如图,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() .
.
请类比(1)中解决问题的思想方法,添加适当的辅助线,判断线段![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°

(1)求证:①AC=BD;②∠APB=50°;
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 ,∠APB的大小为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分的面积是()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com