
 如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$. 分析 首先根据题意画出图形,然后解直角三角形求得AC的长,然后分两种情况讨论即可求得答案.
解答 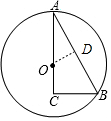 解:当⊙O经过点C时,则AC是直径,
解:当⊙O经过点C时,则AC是直径,
∵Rt△ABC中,∠C=90°,∠A=30°,AB=4,
∴AC=cos30°•AB=2$\sqrt{3}$,
∴OA=$\sqrt{3}$,
当圆O经过B点时,如图,
作OD⊥AB于点D,
∴AD=$\frac{1}{2}$AB=2,
∵∠A=30°,
∴cos∠A=$\frac{AD}{OA}$=$\frac{\sqrt{3}}{2}$,
∴OA=$\frac{4\sqrt{3}}{3}$;
∴⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$,
故答案为$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.
点评 此题考查了直线与圆的位置关系以及解直角三角形.此题难度适中,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
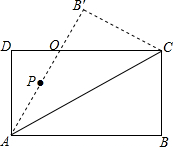 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )| A. | 不变 | B. | 变小 | C. | 变大 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度.
如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
(1)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com