
【题目】如图,抛物线y=ax2﹣2ax+3的图象与x轴分别交于点A,B,与y轴交于点C,已知BO=CO.
(1)求抛物线的解析式;
(2)点E在线段OB上,过点E作x轴的垂线交抛物线于点P,连结PA,若PA⊥CE,垂足为点F,求OE的长.

【答案】(1)抛物线的解析式为y=﹣x2+2x+3;(2)OE的长为![]()
【解析】
(1)利用二次函数图象上点的坐标特征可求出点C的坐标,由OB=OC可得出点B的坐标,根据点B的坐标利用待定系数法即可求出抛物线的解析式;
(2)设PA交y轴于点D,由∠ADO=∠CDF利用等角的余角相等可得出∠PAB=∠OCE,结合∠PEA=∠EOC=90°可得出△PEA∽△EOC,根据相似三角形的性质可得出![]() =
=![]() ,设点E的坐标为(x,0),则点P的坐标为(x,﹣x2+2x+3),进而可得出关于x的方程,解之即可得出结论.
,设点E的坐标为(x,0),则点P的坐标为(x,﹣x2+2x+3),进而可得出关于x的方程,解之即可得出结论.
(1)当x=0时,y=3,∴点C的坐标为(0,3),∴OB=OC=3,∴点B的坐标为(3,0).
∵抛物线y=ax2﹣2ax+3的图象过点B(3,0),∴0=9a﹣6a+3,解得:a=﹣1,∴抛物线的解析式为y=﹣x2+2x+3.
(2)设PA交y轴于点D,如图所示.
∵PA⊥CE,∴∠EFA=∠EOC=90°.
∵∠ADO=∠CDF,∴∠PAB=∠OCE.
∵PE⊥x轴,∴∠PEA=∠EOC=90°,∴△PEA∽△EOC,∴![]() =
=![]() .
.
设点E的坐标为(x,0),则点P的坐标为(x,﹣x2+2x+3),∴![]() =
=![]() ,解得:x=
,解得:x=![]() 或x=-1(舍去),即OE的长为
或x=-1(舍去),即OE的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知射线AP是△ABC的外角平分线,连结PB、PC.
(1)如图1,若BP平分∠ABC,且∠ACB=30°,写出∠APB的度数.
(2)如图1,若P与A不重合,求证:AB+AC<PB+PC.
(3)如图2,若过点P作PM⊥BA,交BA延长线于M点,且∠BPC=∠BAC,求:![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
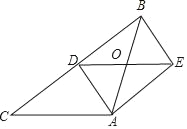
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连结DE,交AB与点O,若BC=8,AO=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )

A. 2﹣![]() B. 2+
B. 2+![]() C. 4﹣
C. 4﹣![]() D. 4+
D. 4+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com