
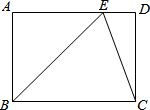
 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.分析 (1)由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=1,根据勾股定理求出BE即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵EC平分∠DEB,
∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC.
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵∠ABE=45°,
∴∠ABE=AEB=45°,
∴AB=AE=1,
由勾股定理得:BE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴BC=BE=$\sqrt{2}$.
点评 本题考查了矩形的性质,等腰三角形的判定,勾股定理的应用;熟练掌握矩形的性质,证出∠BEC=∠ECB是解决问题(1)的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子,所得点数不超过6 | |
| B. | 买一张彩票中奖 | |
| C. | 太阳从西边落下 | |
| D. | 口袋中装有10个红球,从中摸出一个是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
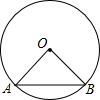 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )| A. | 4 | B. | 2 | C. | $2\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com