
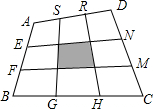
 如图,已知四边形ABCD中E,F,G,H,N、N,R、S分别是四边形三等分点,求证:S阴影=$\frac{1}{9}$S四边形ABCD.
如图,已知四边形ABCD中E,F,G,H,N、N,R、S分别是四边形三等分点,求证:S阴影=$\frac{1}{9}$S四边形ABCD. 分析 连接RN、AC、EH,如图1,易证RN=$\frac{1}{3}$AC=$\frac{1}{2}$EH,RN∥AC∥EH,进而可证到L是EN、RH的三等分点,同理可得I是EN、SG的三等分点,J是SG、FM的三等分点,K是FM、RH的三等分点.要证S阴影=$\frac{1}{9}$S四边形ABCD,只需证S四边形ILKJ=$\frac{1}{3}$S四边形EFMN,S四边形EFMN=$\frac{1}{3}$S四边形ABCD,连接LJ、EJ、LM、EM,如图2,只需运用等高三角形的面积比等于底的比即可解决问题.
解答 证明:连接RN、AC、EH,如图1,
∵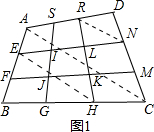 E,F,G,H,N、N,R、S分别是四边形三等分点,
E,F,G,H,N、N,R、S分别是四边形三等分点,
∴$\frac{DR}{DA}$=$\frac{DN}{DC}$=$\frac{1}{3}$,$\frac{BE}{BA}$=$\frac{BH}{BC}$=$\frac{2}{3}$.
∵∠D=∠D,∠EBH=∠ABC,
∴△DRN∽△DAC,△BEH∽△BAC,
∴$\frac{RN}{AC}$=$\frac{DR}{DA}$=$\frac{1}{3}$,$\frac{EH}{AC}$=$\frac{BE}{BA}$=$\frac{2}{3}$,∠DRN=∠DAC,∠BEH=∠BAC,
∴RN=$\frac{1}{2}$EH,RN∥AC,EH∥AC,
∴RN∥EH,
∴△RNL∽△HEL,
∴$\frac{NL}{EL}$=$\frac{RL}{HL}$=$\frac{1}{2}$,
∴L是EN、RH的三等分点.
同理:I是EN、SG的三等分点,J是SG、FM的三等分点,K是FM、RH的三等分点.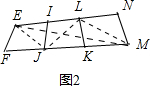 连接LJ、EJ、LM、EM,如图2.
连接LJ、EJ、LM、EM,如图2.
∵L、I是EN的三等分点,
∴S△LIJ=$\frac{1}{2}$S△LEJ,S△ELM=$\frac{2}{3}$S△ENM.
∵J、K是FM的三等分点,
∴S△LKJ=$\frac{1}{2}$S△LJM,S△EJM=$\frac{2}{3}$S△EFM,
∴S四边形ILKJ=S△LIJ+S△LJK
=$\frac{1}{2}$S△LEJ+$\frac{1}{2}$S△LJM=$\frac{1}{2}$S四边形EJML
=$\frac{1}{2}$(S△ELM+S△EJM)
=$\frac{1}{2}$×[$\frac{2}{3}$S△ENM+$\frac{2}{3}$S△EFM]
=$\frac{1}{3}$S四边形EFMN.
同理:S四边形EFMN=$\frac{1}{3}$S四边形ABCD,
∴S阴影=S四边形ILKJ=$\frac{1}{9}$S四边形ABCD.
点评 本题主要考查了相似三角形的判定与性质、平行线的判定与性质、等高三角形的面积比等于底的比等知识,证到L、I是EN的三等分点及J、K是FM的三等分点,并由此证到四边形ILKJ的面积是四边形EFMN面积的三分之一是解决本题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
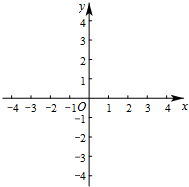 已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=$2\sqrt{5}$.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D.设点P的横坐标为m.
已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=$2\sqrt{5}$.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D.设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com