
 ��֪��ƽ��ֱ������ϵxOy�У���ͼ����������y=ax2-4��x��ĸ������ཻ�ڵ�A����y���ཻ�ڵ�B��AB=$2\sqrt{5}$����P���������ϣ��߶�AP��y��������ύ�ڵ�C���߶�BP��x���ཻ�ڵ�D�����P�ĺ�����Ϊm��
��֪��ƽ��ֱ������ϵxOy�У���ͼ����������y=ax2-4��x��ĸ������ཻ�ڵ�A����y���ཻ�ڵ�B��AB=$2\sqrt{5}$����P���������ϣ��߶�AP��y��������ύ�ڵ�C���߶�BP��x���ཻ�ڵ�D�����P�ĺ�����Ϊm������ ��1���ȸ���y���ϵ����������ȷ��B��0��-4���������ù��ɶ��������OA=2����A������Ϊ��-2��0����Ȼ���A���������y=ax2-4���a��ֵ���ɵõ������߽���ʽ��
��2�����ݶ��κ���ͼ���ϵ��������������P��m��m2-4����m��2�������ֱ��AP�Ľ���ʽ���ɣ�
��3�����ۣ���ֱ��y=-x+b������A��-2��0��ʱ��y=-x+b��ͼ��Gֻ��һ�������㣬��ֱ��y=-x+b������B��0��-4��ʱ��y=-x+b��ͼ��G����2�������㣬�ɴ˿��Եó�b��ȡֵ��Χ������y=-x+b��ͼ��Gֻ��һ�������㣬���÷���-x+b=x2-4�еȸ�����=0���ɣ�
��� �⣺��ͼ��
��1����x=0ʱ��y=ax2-4=-4����B��0��-4��������OB=4��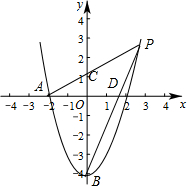
��Rt��OAB��OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{��2\sqrt{5}��^{2}-{4}^{2}}$=2��
��A��������-2��0����
��A��-2��0������y=ax2-4��4a-4=0�����a=1��
�������߽���ʽΪy=x2-4��
��2����P��m��m2-4����m��2����
��ֱ��AP�Ľ���ʽΪy=kx+n��
��A��-2��0����P��m��m2-4�������$\left\{\begin{array}{l}{-2k+n=0}\\{mk+n={m}^{2}-4}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=m-2}\\{n=2m-4}\end{array}\right.$��
��ֱ��AP�Ľ���ʽΪy=��m-2��x+2m-4��
��x=0ʱ��y=��m-2��x+2m-4=2m-4��
��C��0��2m-4����
��OC=2m-4��
��3���ٵ�ֱ��y=-x+b������A��-2��0��ʱֱ����ͼ��GֻҪһ�����㣬2+b=0�����b=-2����ֱ��y=-x+b������B��0��-4��ʱֱ����ͼ��G���������㣬b=-4��
���Ե�-2��b��-4ʱ��y=-x+b��ͼ��Gֻ��һ�������㣻
�ڵ�������$\left\{\begin{array}{l}{y={x}^{2}-4}\\{y=-x+b}\end{array}\right.$��һ���ʱ��y=-x+b��ͼ��Gֻ��һ�������㣬��-x+b=x2-4�еȸ���
���ԡ�=1-4��-4-b��=0�����b=-$\frac{17}{4}$��
������������-2��b��-4��b=-$\frac{17}{4}$ʱ��y=-x+b��ͼ��Gֻ��һ�������㣮
���� ���⿼���˴���ϵ�����������߽���ʽ��һ�κ��������ʡ����ɶ�����֪ʶ�����������ǽ���Ĺؼ��������������е��Ѷȣ�ͨ������㣬ת����˼������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
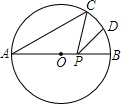 ��ͼ��AB�ǡ�O��ֱ����AB=4����C�ڡ�O�ϣ���CAB=30�㣬DΪ$\widehat{BC}$���е㣬P��ֱ��AB��һ���㣬��PC+PD����СֵΪ��������
��ͼ��AB�ǡ�O��ֱ����AB=4����C�ڡ�O�ϣ���CAB=30�㣬DΪ$\widehat{BC}$���е㣬P��ֱ��AB��һ���㣬��PC+PD����СֵΪ��������| A�� | 2$\sqrt{2}$ | B�� | $\sqrt{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������A��B��������ʾ�����ֱ�Ϊ-2��8��
��ͼ����֪������A��B��������ʾ�����ֱ�Ϊ-2��8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
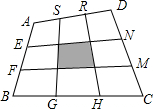 ��ͼ����֪�ı���ABCD��E��F��G��H��N��N��R��S�ֱ����ı������ȷֵ㣬��֤��S��Ӱ=$\frac{1}{9}$S�ı���ABCD��
��ͼ����֪�ı���ABCD��E��F��G��H��N��N��R��S�ֱ����ı������ȷֵ㣬��֤��S��Ӱ=$\frac{1}{9}$S�ı���ABCD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com