
 如图,已知数轴上A、B两点所表示的数分别为-2和8.
如图,已知数轴上A、B两点所表示的数分别为-2和8.分析 (1)根据数轴上两点间距离公式计算可得,即数轴上两点A、B表示的数分别为x1、x2,则AB=|x1-x2|;
(2)当点P在线段AB上时,MN=MP+NP,可根据中点性质得到MP=$\frac{1}{2}$AP、NP=$\frac{1}{2}$BP,相加可得;
(3)当点P在数轴上运动时,可分下面三种情况:
①点P在A、B两点之间运动时,根据MN=MP+NP计算可得,
②点P在点A的左侧运动时,根据MN=NP-MP计算可得,
③点P在点B的右侧运动时,根据MN=MP-NP计算可得,最后综合三种情况得出结论.
解答 解:(1)AB=8-(-2)=lO.
(2)线段MN的长度为5.如图甲,
∵M为AP中点,N为BP的中点,
∴MP=$\frac{1}{2}$AP,NP=$\frac{1}{2}$BP,
∵AB=10,
∴MN=MP+NP=$\frac{1}{2}$AP+$\frac{1}{2}$BP=$\frac{1}{2}$AB=5
(3)线段MN的长度不发生变化,其值为5.分下面三种情况:
①当点P在A、B两点之间运动时(如图甲).MN=MP+NP=$\frac{1}{2}$AP+$\frac{1}{2}$BP=$\frac{1}{2}$AB=5
②当点P在点A的左侧运动时(如图乙).MN=NP-MP=$\frac{1}{2}$BP-$\frac{1}{2}$AP=$\frac{1}{2}$AB=5
③当点P在点B的右侧运动时(如图丙) MN=MP-NP=$\frac{1}{2}$AP-$\frac{1}{2}$BP=$\frac{1}{2}$AB=5
综上所述,线段MN的长度不发生变化,其值为5.
点评 本题考查了线段的计算和中点的性质及数轴的知识,由于引进了数轴,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC的平分线交BC于点D,E为AB上一点,DE=DC,以D为圆心,DB为半径作⊙D.求证:
如图,在Rt△ABC中,∠BAC的平分线交BC于点D,E为AB上一点,DE=DC,以D为圆心,DB为半径作⊙D.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
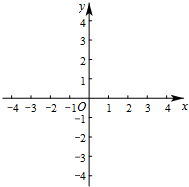 已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=$2\sqrt{5}$.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D.设点P的横坐标为m.
已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=$2\sqrt{5}$.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D.设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
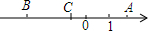 有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:
有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com