
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由.

【答案】(1)证明见解析;(2)垂直,理由见解析.
【解析】
(1)证明△ABD≌△CBE即可得出AD=CE;
(2)延长AD分别交BC和CE于G和F,由于△ABD≌△CBE,所以∠BAD=∠BCE从而可知∠AFC=∠ABC=90°,所以AD⊥CE.
解:(1)∵△ABC和△DBE均为等腰直角三角形
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
在△ABD与△CBE中,
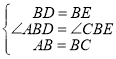 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE.
(2)垂直.延长AD分别交BC和CE于G和F,
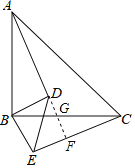
∵△ABD≌△CBE,
∵∠BAD=∠BCE,
又∵∠BGA=∠CGF,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,梯形![]() 的顶点
的顶点![]() 、
、![]() 在反比例函数
在反比例函数![]() 图像上,
图像上,![]() ,上底边
,上底边![]() 在直线
在直线![]() 上,下底边
上,下底边![]() 交
交![]() 轴于
轴于![]() ,点
,点![]() 的纵坐标是1.
的纵坐标是1.
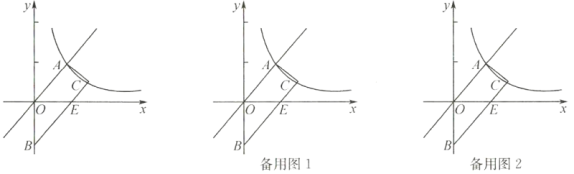
(1)求反比例函数的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,其他条件不变,探究四边形
,其他条件不变,探究四边形![]() 的面积;
的面积;
(4)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,点
,点![]() 的纵坐标改为
的纵坐标改为![]() ,且
,且![]() ,其他条件不变,直接写出四边形
,其他条件不变,直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】豫让桥豫东市场某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个.若销售单价每个降低2元,则每周可多卖出20个;若商户计划下周利润达到5200元,则此电子产品的售价为每个多少元?设销售价格每个降低x元(x为偶数),则所列方程为( )
A. (80﹣x)(160+20x)=5200 B. (30﹣x)(160+20x)=5200
C. (30﹣x)(160+10x)=5200 D. (50﹣x)(160+10x)=5200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在一次测验中解答的填空题:①若x2=a2,则x=a;②方程2x(x-1)-x+1=0的解是x=1;③已知三角形两边分别为2和9,第三边长是方程x2-14x+48=0的根,则这个三角形的周长是17或19.其中答案完全正确的题目个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知P是半径为5cm的⊙O内一点.解答下列问题:

(1)用尺规作图找出圆心O的位置.(要求:保留所有的作图痕迹,不写作法)
(2)用三角板分别画出过点P的最长弦AB和最短弦CD.
(3)已知OP=3cm,过点P的弦中,长度为整数的弦共有 _________ 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

【答案】![]()
【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点![]() ,
,
![]() ,
,
![]() 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
![]() 点P的坐标为
点P的坐标为![]() .
.
故答案为:![]() .
.
【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() 。
。
(1)请画出![]() 关于
关于![]() 轴对称后得到的
轴对称后得到的![]() ;
;
(2)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(3)在![]() 轴上寻找一个点
轴上寻找一个点![]() ,使
,使![]() 的周长最小,并直接写出
的周长最小,并直接写出![]() 的周长的最小值。
的周长的最小值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com