【题目】已知y关于x的函数表达式是
，下列结论不正确的是（ ）
A.若
，函数的最大值是5
B.若
，当
时，y随x的增大而增大
C.无论a为何值时，函数图象一定经过点
D.无论a为何值时，函数图象与x轴都有两个交点
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】如图，点O在∠APB的平分线上，⊙O与PA相切于点C．
（1）求证：直线PB与⊙O相切；
（2）PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
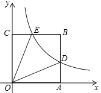
【题目】平面直角坐标系中，正方形OABC如图放置，反比例函数
的图像交AB于点D，交BC于点E，已知A（
，0），∠DOE=30°，则k的值为（ ）
A.
B.C.3D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】茶叶是安徽省主要经济作物之一，2020年新茶上市期间，某茶厂为获得最大利益，根据市场行情，把新茶价格定为400元/kg，并根据历年的相关数据整理出第x天（1≤x≤15，且x为整数）制茶成本（含采摘和加工）和制茶量的相关信息如下表．假定该茶厂每天制作和销售的新茶没有损失，且能在当天全部售出（当天收入=日销售额-日制茶成本）
制茶成本（元/kg） | 150+10x |
制茶量（kg） | 40+4x |
（1）求出该茶厂第10天的收入；
（2）设该茶厂第x天的收入为y（元）．试求出y与x之间的函数关系式，并求出y的最大值及此时x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
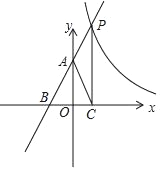
【题目】已知，如图所示直线y=kx+2（k≠0）与反比例函数y=
（m≠0）分别交于点P，与y轴、x轴分别交于点A和点B，且cos∠ABO=
，过P点作x轴的垂线交于点C，连接AC，
（1）求一次函数的解析式．
（2）若AC是△PCB的中线，求反比例函数的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解朝阳社区
岁居民最喜欢的支付方式，某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图．请根据图中信息解答下列问题：
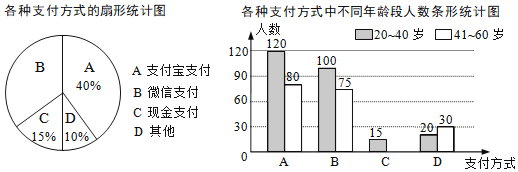
（1）求参与问卷调查的总人数．
（2）补全条形统计图．
（3）该社区中岁的居民约8000人，估算这些人中最喜欢微信支付方式的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道
上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=300，∠CBD=600．
(1)求AB的长(精确到0.1米，参考数据：
)；
(2)已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由．
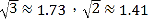
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，线段
及一定点
，
是线段上一动点（
、
除外），作直线
，使
于点，作直线
，使
于点
.已知
，
，设
，
，数学学习小组根据学习函数的经验，对
与
之间的内在关系进行探究.
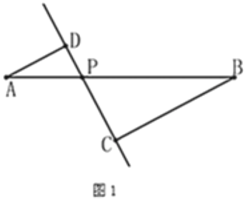
（1）写出y与之间的关系和的取值范围；
活动操作：
（2）①列表，根据（1）的所求函数关系式讲算并补全表格
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
|
| 1.8 | 9 | 21 |
②描点：根据表格中数值，继续在图2中描出剩余的三个点
；
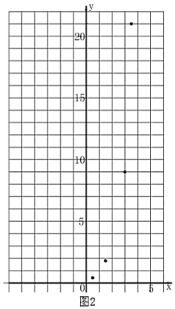
③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象.
数学思考：
（3）请你结合函数的图象，写出该函数的一条性质或结论.
（4）将该函数图象向上移3个单位，再向左平移4个单位后，直接写出平移后的函数关系式和的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
