
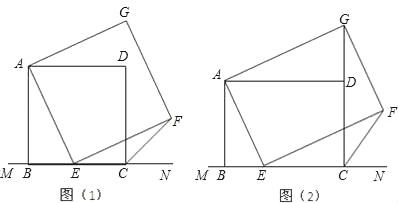
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
【答案】(1)见解析;(2)45°;(3)![]() .
.
【解析】试题分析:
(1)由正方形的性质,用SAS证明△BAE≌△DAG;
(2)作FH⊥MN于H,证明△EFH≌△ABE,再证△CHF是等腰直角三角形;
(3)结合(1)(2),可证明△EFH≌△GAD,△EFH∽△ABE,再用相似三角形的性质得到结论.
试题解析:
(1)证明:∵四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE+∠EAD=∠DAG+∠EAD,
∴∠BAE=∠DAG,
∴△BAE≌△DAG.
(2)解:∠FCN=45°,
理由是:作FH⊥MN于H,
∵∠AEF=∠ABE=90°,
∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,
又∵AE=EF,∠EHF=∠EBA=90°,
∴△EFH≌△ABE,
∴FH=BE,EH=AB=BC,
∴CH=BE=FH,
∵∠FHC=90°,
∴∠FCN=45°.
(3)解:当点E由B向C运动时,∠FCN的大小总保持不变,
理由是:作FH⊥MN于H,
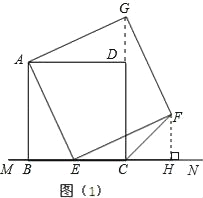
由已知可得∠EAG=∠BAD=∠AEF=90°,
结合(1)(2)得∠FEH=∠BAE=∠DAG,
又∵G在射线CD上,
∠GDA=∠EHF=∠EBA=90°,
∴△EFH≌△GAD,△EFH∽△ABE,
∴EH=AD=BC=b,
∴CH=BE,
∴![]() ;
;
在Rt△FEH中,tan∠FCN=![]() ,
,
∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款2.4万元,乙工程队工程款1万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用12天;
(3)若甲,乙两队合做6天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
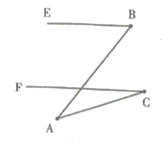
【题目】如图(a),木杆EB与FC平行,木杆的两端B,C用一橡皮筋连接,现将图(a)中的橡皮筋拉成下列各图的形状,试解答下列各题:

(1)探究图(b)、(c)、(d)、(e)中,![]() 之间的数量关系,并填空;
之间的数量关系,并填空;
①图(b)中,![]() 之间的关系是________________________;
之间的关系是________________________;
②图(c)中,![]() 之间的关系是_________________________;
之间的关系是_________________________;
③图(d)中,![]() 之间的关系是__________________________;
之间的关系是__________________________;
④图(e)中,![]() 之间的关系是__________________________;
之间的关系是__________________________;
(2)探究图(f)、(g)中,![]() 之间的数量关系,并填空:
之间的数量关系,并填空:
①图(f)中,![]() 之间的关系是________________________________;
之间的关系是________________________________;
②图(g)中,![]() 之间的关系是________________________________;
之间的关系是________________________________;
(3)请对图(e)的结论加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠BAD, ∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=62°,则∠BEF的度数为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
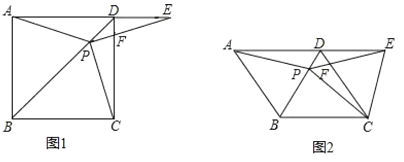
【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=![]() AP;
AP;
(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题目要求解答下列各题
(1)在图1中画出△ABC关于Y轴对称的△A1B1C1
(2)直接写出△ABC关于X轴对称的△A2B2C2的各点坐标.![]() ,
,![]() ,
,![]()
(3)在图2中的Y轴上确定点P的位置,使PA+PB最小

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com