
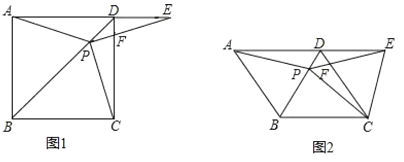
【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=![]() AP;
AP;
(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
【答案】(1)证明见解析;(2)证明见解析;(3)AP=CE.
【解析】
(1)根据正方形性质知道PC=PA,又由PE=PC知道PA=PE即可得出结论.
(2)证明△PEC为等腰直角三角形,即可得出结论.
(3)根据(2)的思路和方法即可求出结论AP=CE.
(1)证明:在正方形ABCD中,AD=DC,
∠ADP=∠CDP=45°,
在△ADP和△CDP中,AD=DC;∠ADP=∠CDP;PD=PD,
∴△ADP≌△CDP(SAS),
∴∠DAP=∠DCP,PA=PC;
∵PC=PE,
∴PA=PE,
∴∠DAP=∠DEP,
∴∠DCP=∠DAP=∠DEP.
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
∴△CPE是等腰直角三角形,
∴EC=![]() CP,
CP,
又∵AP=CP,
∴EC=![]() AP.
AP.
(3)AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,AB=BC;∠ABP=∠CBP;PB=PB,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.


科目:初中数学 来源: 题型:
【题目】已知点B、C为线段AD上的两点,AB=![]() BC=
BC=![]() CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
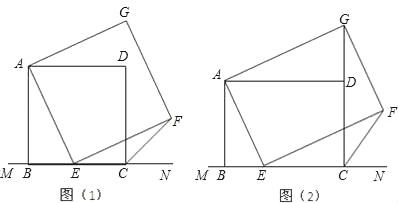
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”,这批单车分为A、B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动,投放A、B两种款型的单车共100辆,总价值36800元.求本次试点投放的A型车、B型车的辆数.
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A、B两车型的数量比进行投放,且投资总价值不低于184万元.问整个城区全面铺开时投放的A型车、B型车至少多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑电动车从A地到B地,乙骑自行车从B地到A地,两人同时出发,设乙骑自行车的时间为t(h),两人之间的距离为s(km),图中的折线表示s和t之间的关系,根据图象回答下列问题.
(1)A、B两地之间的距离为 km;
(2)求甲出发多长时间与乙相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,点 A( 2,2)、B(0,1)点 P 在 x 轴上,且△PAB 的等腰三角形,则满足条件的点 P 共有()个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com