
【题目】某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q = W + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
次数n | 2 | 1 |
速度x | 40 | 60 |
指数Q | 420 | 100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
【答案】(1) ![]() ;(2) n=2;(3)90;(4)能,m=50.
;(2) n=2;(3)90;(4)能,m=50.
【解析】(1)根据题目所给的信息,设W=k1x2+k2nx,然后根据Q=W+100,列出用Q的解析式;(2)将x=70,Q=450,代入求n的值即可;(3)把n=3代入,确定函数关系式,然后求Q最大值时x的值即可;(4)根据题意列出关系式,求出当Q=420时m的值即可.
解:(1)设![]() ,
,
∴![]() .
.
由表中数据,得![]() ,解得
,解得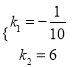
∴![]() .
.
(2)由题意,得![]() .
.
∴n=2.
(3)当n=3时, ![]() .
.
由![]() 可知,要使Q最大,
可知,要使Q最大, 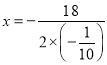 =90.
=90.
(4)由题意,得
![]()
即![]() ,解得
,解得![]() ,或
,或![]() =0(舍去)
=0(舍去)
∴m=50.
“点睛”本题考查了二次函数的应用,难度较大,解答本题的关键是根据题目中所给的信息,读懂题意列出函数关系式,要求同学们掌握求二次函数最值的方法,此题较麻烦,考查学生利用数学知识解决实际问题的能力.


科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A.明天我市下雨
B.抛一枚硬币,正面朝下
C.购买一张福利彩票中奖了
D.掷一枚骰子,向上一面的数字一定大于零
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过秒后,△BPD≌△CQP. 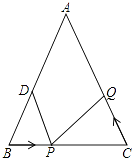
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC的外侧作直线BD,作点A关于直线BD的对称点A′,连接AA′交直线BD于点E,连接A′C交直线BD于点F.
(1)依题意补全图1,已知∠ABD=30°,求∠BFC的度数; 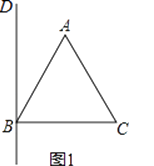
(2)如图2,若60°<∠ABD<90°,判断直线BD和A′C相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )
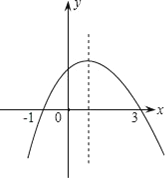
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的内部有一点P,在射线OA,OB边上各取一点P1 , P2 , 使得△PP1P2的周长最小,作出点P1 , P2 , 叙述作图过程(作法),保留作图痕迹. 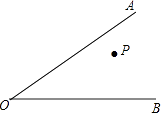
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若x2-2xy+2y2-8y+16=0,求x、y的值.
解:∵x2-2xy+2y2-8y+16=0,
∴(x2-2xy+y2)+(y2-8y+16)=0
∴(x-y)2+(y-4)2=0,
∴(x-y)2=0,(y-4)2=0,
∴y=4,x=4.
根据你的观察,探究下面的问题:
已知a、b满足a2+b2-4a-6b+13=0.求a、b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com