
| x2+9 |
| (16-x)2+81 |
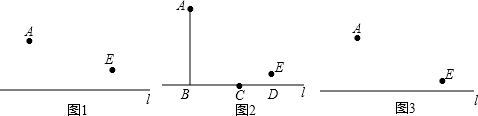
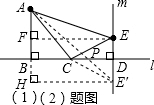
| AE2-AF2 |
| 172-82 |
| AB2+BC2 |
| 81+(15-x)2 |
| DE2+CD2 |
| 1+x2 |
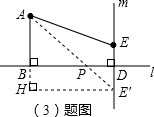
| 81+(15-x)2 |
| 1+x2 |
| AH2+AE′2 |
| 102+152 |
| 13 |
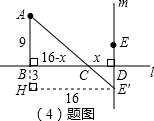
| x2+9 |
| (16-x)2+81 |
| 122+162 |
| x2+9 |
| (16-x)2+81 |


科目:初中数学 来源: 题型:
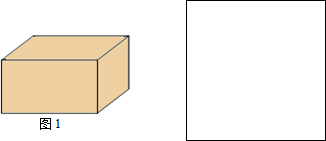
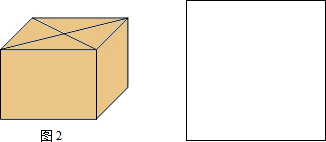

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形OABC放置在第一象限内,已知A(3,0),∠AOB=30°,反比例函数y=
如图,矩形OABC放置在第一象限内,已知A(3,0),∠AOB=30°,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 含A:x(kg) | 5 | 15 |
| 出厂价(元/50kg) | 2450 | 2350 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线m∥n,直线m,n和直线AB分别交于A、B 两点,直线m,n和直线CD分别交于C、D 两点.点P在直线AB上.∠1是线段CP与CA的夹角,∠2是线段DP与DB的夹角,∠3是线段PC与PD的夹角.
如图,已知直线m∥n,直线m,n和直线AB分别交于A、B 两点,直线m,n和直线CD分别交于C、D 两点.点P在直线AB上.∠1是线段CP与CA的夹角,∠2是线段DP与DB的夹角,∠3是线段PC与PD的夹角.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
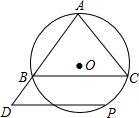 如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是圆上的一个动点,过点P作BC的平行线交AB的延长线于点D.
如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是圆上的一个动点,过点P作BC的平行线交AB的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、(x-3)2=
| ||
B、3(x-1)2=
| ||
C、(x-1)2=
| ||
| D、(3x-1)2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com