
【题目】如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;
③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( )
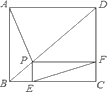
A. ①② B. ①④ C. ①②④ D. ①③④
【答案】C
【解析】如图,

∵P为正方形ABCD的对角线BD上任一点,
∴PA=PC,∠C=90°,
∵过点P作PE⊥BC于点E,PF⊥CD,
∴∠PEC=∠DFP=∠PFC=∠C=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴PA=EF,故②正确,
∵BD是正方形ABCD的对角线,
∴∠ABD=∠BDC=∠DBC=45°,
∵∠PFC=∠C=90°,
∴PF∥BC,
∴∠DPF=45°,
∵∠DFP=90°,
∴△FPD是等腰直角三角形,故①正确,
在△PAB和△PCB中,
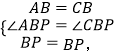 ,
,
∴△PAB≌△PCB,
∴∠BAP=∠BCP,
在矩形PECF中,∠PFE=∠FPC=∠BCP,
∴∠PFE=∠BAP.故④正确,
∵点P是正方形对角线BD上任意一点,
∴AD不一定等于PD,
只有∠BAP=22.5°时,AD=PD,故③错误,
故选C


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y![]() 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用:

(1)如图,可以求出阴影部分的面积是_____(写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_____,长是_____,面积是________(写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式:_________(用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
![]()
A. 点E B. 点F C. 点M D. 点N
查看答案和解析>>
科目:初中数学 来源: 题型:
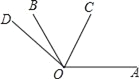
【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个
![]()
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图所示的计算程序.
![]()
根据计算程序回答下列问题:
(1)填写表内空格:
输入x | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是 .
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com