
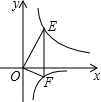
 如图,直线EF∥y轴,分别交双曲线y=$\frac{8}{x}$(x>0和y=-$\frac{2}{x}$(x>0)的图象于E、F,且OE⊥OF,则EF=5.
如图,直线EF∥y轴,分别交双曲线y=$\frac{8}{x}$(x>0和y=-$\frac{2}{x}$(x>0)的图象于E、F,且OE⊥OF,则EF=5. 分析 过点E作EA⊥y轴,垂足为A,过点F作FB⊥y轴,垂足为B,从而求得OA=$\frac{8}{x}$,OB=$\frac{2}{x}$.然后证明△AEO∽△BOF,接下来根据相似三角形的性质可求得x=2,从而可求得OA=4,OB=1,从而可求得EF=5.
解答 解:过点E作EA⊥y轴,垂足为A,过点F作FB⊥y轴,垂足为B.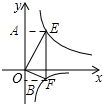
由反比例函数的几何意义可知:OA=$\frac{8}{x}$,OB=$\frac{2}{x}$.
∵OE⊥OF,
∴∠BOF+∠AOE=90°.
又∵∠AOE+∠OEA=90°,
∴∠BOF=∠OEA.
又∵∠OAE=∠OBF,
∴△AEO∽△BOF.
∴$\frac{AE}{OA}=\frac{OB}{BF}$,即AE•BF=OA•OB.
∴${x}^{2}=\frac{8}{x}•\frac{2}{x}$.
解得:x=2(负值已舍去).
∴EF=OA+OB=$\frac{8}{2}+\frac{2}{2}$=5.
故答案为:5.
点评 本题主要考查的是反比例函数的性质、相似三角形的性质和判定,列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ac>bc | B. | -$\frac{1}{2}$a>-$\frac{1}{2}$b | C. | a+1<1+b | D. | 3a>3b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com