练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

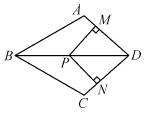
    如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M、N.

    (1)求证：∠ADB＝∠CDB；

    (2)若∠ADC＝90°，求证：四边形MPND是正方形.


    证明：(1)∵BD平分∠ABC，

    ∴∠ABD＝∠CBD.

    又∵BA＝BC，BD＝BD，∴△ABD≌△CBD，

    ∴∠ADB＝∠CDB.

    (2)∵PM⊥AD，PN⊥CD，

    ∴∠PMD＝∠PND＝90°.

    又∵∠ADC＝90°，∴四边形MPND是矩形.

    ∵∠ADB＝∠CDB，PM⊥AD，PN⊥CD，

    ∴PM＝PN，

    ∴四边形MPND是正方形.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷（解析版） 题型：选择题

    下列银行标志中，不是轴对称图形的是（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，平行四边形ABCD的对角线AC,BD交于点O，E,F在AC上，G,H在BD上，且AF=CE，BH=DG.求证：四边形EGFH为平行四边形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


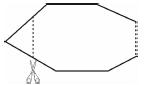
    如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2 340°的新多边形，则原多边形的边数为(     )

    A.13            B.14            C.15                D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF.求证：AF=CE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为(     )

      A.1            B.2            C.3           D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知□ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使□ABCD成为一个菱形.你添加的条件是                    .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    圆的对称性

    圆的对称性

    圆是轴对称图形，其对称轴是任意一条经过⑦          的直线.

    圆是中心对称图形，对称中心为⑧          .

    垂径定理

    定理

    垂直于弦的直径⑨          弦，并且平分弦所对的两条⑩          .

    推论

    平分弦(不是直径)的直径⑪          弦，并且⑫          弦所对的两条弧.

    圆心角、弧、弦之间的关系

    在同圆或等圆中，如果两个圆心角﹑两条弧或两条弦中有一组量⑬          ，那么它们所对应的其余各组量也分别相等.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


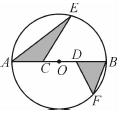
    如图，半径为6 cm的⊙O中，C、D为直径AB的三等分点，点E、F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连接AE、BF，则图中两个阴影部分的面积为          cm2.

    查看答案和解析>>

    同步练习册答案