练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点E在线段BC上，AB⊥BC，DC⊥BC，∠AED＝90°，且AE＝DE．

    （1）求证：△ABE≌△ECD．

    （2）直接写出线段AB、BC、CD之间的数量关系．

    【答案】（1）见解析；（2）BC＝AB+CD

    【解析】

    （1）因为AB⊥BC，DC⊥BC，则∠B＝∠C＝∠AED＝90°，故∠A+∠AEB＝90°，再结合题意得到∠A＝∠DEC，由“AAS”可证△ABE≌△ECD；

    （2）由全等三角形的性质可得CE＝AB，BE＝CD，即可求解．

    证明：（1）∵AB⊥BC，DC⊥BC，

    ∴∠B＝∠C＝∠AED＝90°，

    ∴∠A+∠AEB＝90°，∠AEB+∠DEC＝90°，

    ∴∠A＝∠DEC，

    在△ABE和△ECD中

    ∴△ABE≌△ECD（AAS）；

    （2）∵△ABE≌△ECD

    ∴CE＝AB，BE＝CD，

    ∴BC＝BE+CE＝AB+CD．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

    （1）求证：AB=CF；

    （2）连接DE，若AD=2AB，求证：DE⊥AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC＝90°，AB＝AC．点D从点B出发沿射线BC移动，以AD为边在AB的右侧作△ADE，且∠DAE＝90°，AD＝AE．连接CE．

    （1）如图1，若点D在BC边上，则∠BCE＝　 °；

    （2）如图2，若点D在BC的延长线上运动．

    ①∠BCE的度数是否发生变化？请说明理由；

    ②若BC＝3，CD＝6，则△ADE的面积为　 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC＝15，且△ABC的面积为90，D是线段AB上的动点（包含端点），若线段CD的长为正整数，则点D的个数共有（　　）

    A.2个B.3个C.4个D.5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC和△ECD都是等边三角形，B、C、D三点在一条直线上，AD与BE相交于点O，AD与CE相交于点F，AC与BE相交于点G．

    （1）△BCE与△ACD全等吗？请说明理由．

    （2）求∠BOD度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.

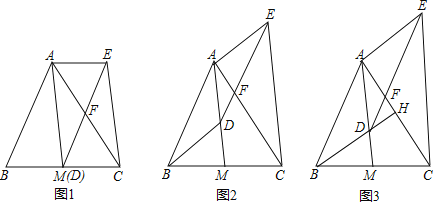
    (1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;

    (2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.

    (3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM

    ①求∠CAM的度数;

    ②当FH=, DM=4时,求DH的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，函数y=（k＞0，x＞0）的图象经过菱形OACD的顶点D和边AC的中点E，若菱形OACD的边长为3，则k的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与x轴交于点C，与y轴交于点B，点A（1，3），点B（0，2）．连接AO

    （1）求直线AB的解析式；

    （2）求三角形AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在锐角△ABC中，AC是最短边．以AC为直径的⊙O，交BC于D，过O作OE∥BC，交OD于E，连接AD、AE、CE．

    （1）求证：∠ACE=∠DCE；

    （2）若∠B=45°，∠BAE=15°，求∠EAO的度数；

    （3）若AC=4，，求CF的长．

    查看答案和解析>>

    同步练习册答案