
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 ![]() .
.
(1)求证:∠BAE=∠CAD;
(2)求证:△ABE∽△ACD.
【答案】
(1)证明:在△ABC与△AED中,
∵ ![]() ,
,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC﹣∠EAF=∠EAD﹣∠EAF,
即∠BAE=∠CAD;
(2)解:∵ ![]() ,
,
∴ ![]() ,
,
在△ABE与△ACD中,
∵∠BAE=∠CAD, ![]() ,
,
∴△ABE∽△ACD.
【解析】(1)根据相似三角形的判定方法三边对应成比例,两三角形相似,得到△ABC∽△AED,得到对应角相等,根据角的和差证明出∠BAE=∠CAD;(2)根据比例的性质得到两边对应成比例,再由夹角相等,得到两三角形相似.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校的北大门是由相同菱形框架组成的伸缩电动推拉门,如图是大门关闭时的示意图,此时 菱形的边长为0.5m,锐角都是50°.求大门的宽(结果精确到0.01,参考数据:sin25°≈0.422 6,cos25°≈0.906 3).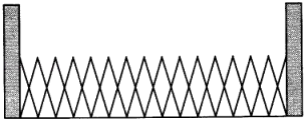
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走的路程![]() 单位:千米
单位:千米![]() 与时间
与时间![]() 单位:时
单位:时![]() 的变量关系的图象.根据图象回答问题:
的变量关系的图象.根据图象回答问题:
![]() 在这个变化过程中,自变量是______ ,因变量是______ .
在这个变化过程中,自变量是______ ,因变量是______ .
![]() 时所走的路程是多少?他休息了多长时间?
时所走的路程是多少?他休息了多长时间?
![]() 他从休息后直至到达目的地这段时间的平均速度是多少?
他从休息后直至到达目的地这段时间的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 3
cm B. 3![]() cm C. 4
cm C. 4![]() cm D. 3cm
cm D. 3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
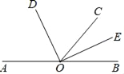
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:DC=BE;
(2)连接BF,若BF⊥AE,求证:△ADF≌△ECF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)求医用口罩和洗手液的单价;
(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com