练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题：①如果3、4、5为一组勾股数，那么3k、4k、5k仍是勾股数；②含有45°角的直角三角形的三边长之比是1∶1:；③如果一个三角形的三边是9，12，13，那么此三角形是直角三角形；④一个直角三角形的两边长是3和4，它的斜边是5．其中正确的个数是 ( )

    A.1个B.2个C.3个D.4个

    【答案】A

    【解析】

    一般地,如果a,b,c是一组勾股数,那么ak,bk,ck(k是正整数)也方式一组勾股数;根据勾股定理和逆定理进行分析.

    ①如果3、4、5为一组勾股数，那么3k、4k、5k仍是勾股数；应(k是正整数)，错误；

    ②含有45°角的直角三角形的三边长之比是1∶1:；正确；

    ③如果一个三角形的三边是9，12，13，那么此三角形是直角三角形；92+122≠132；错误；

    ④一个直角三角形的两边长是3和4，它的斜边不一定是5；故错误.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知如图，△ABC在平面直角坐标系XOY中，其中A（1，2），B（3，1），C（4，3），试解答下列各题：

    （1）作出△ABC关于x轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标；A1（________）；B1（________）；C1（________）．

    （2）作出△ABC关于直线a对称的△A2B2C2，并写出△A2B2C2三个顶点的坐标；A2（________）；B2（________）；C2（________）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在□ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF．

    （1）求证：四边形DEBF是矩形；

    （2）若AF平分∠DAB，AE＝3，BF＝4，求□ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又继续航行7海里后，在B处测得小岛P的方位是北偏东60°，求：

    （1）此时轮船与小岛P的距离BP是多少海里；

    （2）小岛点P方圆3海里内有暗礁，如果轮船继续向东行使，请问轮船有没有触焦的危险？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学校开展的数学活动课上，小明和小刚制作了一个正三楼锥（质量均匀，四个面完全相同），并在各个面上分别标记数字1，2，3，4，游戏规则如下每人投掷三棱锥两次，并记录底面的数字，如果两次所掷数字的和为单数，那么算小明赢，如果两欢所掷数字的和为偶数，那么算小明赢；

    （1）请用列表或者面树状围的方法表示上述游戏中的所有可能结果．

    （2）请分别隶出小明和小刚能赢的概率，并判新游戏的公平性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x轴上，且∠ACB=90°，AC=BC．

    （1）如图1，当A（0，-2），C（1，0），点B在第四象限时，求点B的坐标；
    （2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断是一个定值，并说明定值是多少？请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形例如:某三角形三边长分别是5，6和8，因为，所以这个三角形是常态三角形.

    (1)若△ABC三边长分别是2，和4，则此三角形 常态三角形(填“是”或“不是”);

    (2)如图，Rt△ABC中，∠ACB=90°，BC=6，点D为AB的中点，连接CD，CD=AB， 若△ACD是常态三角形，求△ABC的面积;，

    (3)若Rt△ABC是常态△，斜边是，则此三角形的两直角边的和= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此规律，将△OAB进行n次变换，得到△OAnBn。推测An的坐标是___________，Bn的坐标是___________。（ ）

    A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

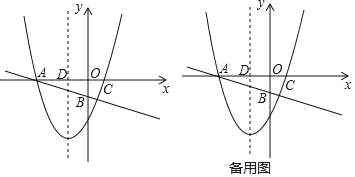
    【题目】如图，在直角坐标系中，直线y=﹣x﹣1与x轴，y轴的交点分别为A、B，以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C，直线x=﹣1与x轴交于点D．

    （1）求抛物线的解析式；

    （2）在线段AB上是否存在一点P，使以A，D，P为顶点的三角形与△AOB相似？若存在，求出点P的坐标；如果不存在，请说明理由；

    （3）若点Q在第三象限内，且tan∠AQD=2，线段CQ是否存在最小值，如果存在直接写出最小值；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案