
ЁОЬтФПЁПЮвУЧаТЖЈвхвЛжжШ§НЧаЮ:СНБпЦНЗНКЭЕШгкЕкШ§БпЦНЗНЕФ4БЖЕФШ§НЧаЮНазіГЃЬЌШ§НЧаЮР§Шч:ФГШ§НЧаЮШ§БпГЄЗжБ№ЪЧ5ЃЌ6КЭ8ЃЌвђЮЊ![]() ЃЌЫљвдетИіШ§НЧаЮЪЧГЃЬЌШ§НЧаЮ.
ЃЌЫљвдетИіШ§НЧаЮЪЧГЃЬЌШ§НЧаЮ.

(1)ШєЁїABCШ§БпГЄЗжБ№ЪЧ2ЃЌ![]() КЭ4ЃЌдђДЫШ§НЧаЮ ГЃЬЌШ§НЧаЮ(ЬюЁАЪЧЁБЛђЁАВЛЪЧЁБ);
КЭ4ЃЌдђДЫШ§НЧаЮ ГЃЬЌШ§НЧаЮ(ЬюЁАЪЧЁБЛђЁАВЛЪЧЁБ);
(2)ШчЭМЃЌRtЁїABCжаЃЌЁЯACB=90ЁуЃЌBC=6ЃЌЕуDЮЊABЕФжаЕуЃЌСЌНгCDЃЌCD=![]() ABЃЌ ШєЁїACDЪЧГЃЬЌШ§НЧаЮЃЌЧѓЁїABCЕФУцЛ§;ЃЌ
ABЃЌ ШєЁїACDЪЧГЃЬЌШ§НЧаЮЃЌЧѓЁїABCЕФУцЛ§;ЃЌ
(3)ШєRtЁїABCЪЧГЃЬЌЁїЃЌаББпЪЧ![]() ЃЌдђДЫШ§НЧаЮЕФСНжБНЧБпЕФКЭ= .
ЃЌдђДЫШ§НЧаЮЕФСНжБНЧБпЕФКЭ= .
ЁОД№АИЁП(1)ЪЧЃЛ(2)![]() Лђ
Лђ![]() ЃЛ(3) 2
ЃЛ(3) 2![]() +4.
+4.
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгРћгУГЃЬЌШ§НЧаЮЕФЖЈвхХаЖЯМДПЩЃЛ
ЃЈ2ЃЉЩшCD=AD=BD=xЃЌРћгУЙДЙЩЖЈРэЧѓГіAC2=4x2-36ЃЌШЛКѓИљОнГЃЬЌШ§НЧаЮЕФЖЈвхЗжЧщПіСаЗНГЬЧѓГіxЃЌНјЖјПЩЕУACЕФГЄЃЌзюКѓРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтЃЛ
ЃЈ3ЃЉгЩЙДЙЩЖЈРэКЭГЃЬЌШ§НЧаЮЕФЖЈвхЕУЃКa2+b2=c2ЃЌa2+c2=4b2ЃЌЧѓГіaЃКb=![]() ЃЌШЛКѓЩшЮДжЊЪ§БэЪОГіcЕФГЄЃЌМДПЩЧѓГіaЃЌbЕФГЄЃЌНјЖјЕУГіД№АИЃЎ
ЃЌШЛКѓЩшЮДжЊЪ§БэЪОГіcЕФГЄЃЌМДПЩЧѓГіaЃЌbЕФГЄЃЌНјЖјЕУГіД№АИЃЎ
(1)Ёп![]() ЃЌ
ЃЌ
ЁрДЫШ§НЧаЮЪЧГЃЬЌШ§НЧаЮЃЛ
ЃЈ2ЃЉЁпRtЁїABCжаЃЌЁЯACB=90ЁуЃЌBC=6ЃЌЕуDЮЊABЕФжаЕуЃЌ
ЁрCD=AD=BD=![]() ABЃЌ
ABЃЌ
ЩшCD=AD=BD=![]() AB=xЃЌдђAB=2xЃЌ
AB=xЃЌдђAB=2xЃЌ
гЩЙДЙЩЖЈРэЕУЃКAC2+62=ЃЈ2xЃЉ2ЃЌ
ЁрAC2=4x2-36ЃЌ
ЂйЁпЁїACDЪЧГЃЬЌШ§НЧаЮЃЌ
ЁрCD2+AD2=4AC2ЃЌ
Ёрx2+x2=4ЃЈ4x2-36ЃЉЃЌ
Ёрx2=![]() ЃЌ
ЃЌ
ЁрAC2=![]()
ЁрAC=![]() ЃЌ
ЃЌ
ЁрЁїABCЕФУцЛ§ЮЊЃК![]() ЁСACЁСBC=
ЁСACЁСBC=![]() ЃЛ
ЃЛ
ЂкЁпЁїACDЪЧГЃЬЌШ§НЧаЮЃЌ
ЁрCD2+AC2=4AD2ЃЌ
Ёрx2+AC2=4x2ЃЌ
ЁрAC2=3x2ЃЌ
ПЩЕУ![]() ЃЛ
ЃЛ
НтЕУЃКx=6ЃЌ
ЁрAC=![]() ЃЌ
ЃЌ
ЁрЁїABCЕФУцЛ§ЮЊЃК![]() ЁСACЁСBC=
ЁСACЁСBC=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЁїABCЕФУцЛ§ЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпRtЁїABCЪЧГЃЬЌШ§НЧаЮЃЌ
ЩшЦфСНжБНЧБпЗжБ№ЮЊЃКaЃЌbЃЌаББпЮЊcЃЌ
дђгЩЙДЙЩЖЈРэКЭГЃЬЌШ§НЧаЮЕФЖЈвхЕУЃКa2+b2=c2ЃЌa2+c2=4b2ЃЌ
Ёр2a2=3b2ЃЌ
ЁрaЃКb=![]() ЃЌ
ЃЌ
Щшa=![]() xЃЌb=
xЃЌb=![]() xЃЌ
xЃЌ
дђc=![]() xЃЌ
xЃЌ
ЁпаББпЪЧ2![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКx=![]() ЃЌ
ЃЌ
Ёрa+b=![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌЁЯABKЕФНЧЦНЗжЯпBEЕФЗДЯђбгГЄЯпКЭЁЯDCKЕФНЧЦНЗжЯпCFЕФЗДЯђбгГЄЯпНЛгкЕуHЃЌЁЯKЉЁЯH=27ЁуЃЌдђЁЯK=ЃЈЁЁЁЁЃЉ

A. 76Ёу B. 78Ёу C. 80Ёу D. 82Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇЩњЕФбЇвЕИКЕЃЙ§жиЛсбЯжигАЯьбЇЩњЖдД§бЇЯАЕФЬЌЖШЃЎЮЊДЫЮвЪаНЬг§ВПУХЖдВПЗжбЇаЃЕФАЫФъМЖбЇЩњЖдД§бЇЯАЕФЬЌЖШНјааСЫвЛДЮГщбљЕїВщЃЈАббЇЯАЬЌЖШЗжЮЊШ§ИіВуМЖЃЌAМЖЃКЖдбЇЯАКмИааЫШЄЃЛBМЖЃКЖдбЇЯАНЯИааЫШЄЃЛCМЖЃКЖдбЇЯАВЛИааЫШЄЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩЭМЂйКЭЭМЂкЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉДЫДЮГщбљЕїВщжаЃЌЙВЕїВщСЫ УћбЇЩњЃЛ
ЃЈ2ЃЉНЋЭМЂйВЙГфЭъећЃЛ
ЃЈ3ЃЉЧѓГіЭМЂкжаCМЖЫљеМЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉИљОнГщбљЕїВщНсЙћЃЌЧыФуЙРМЦЮвЪаНќ8000УћАЫФъМЖбЇЩњжаДѓдМгаЖрЩйУћбЇЩњбЇЯАЬЌЖШДяБъЃЈДяБъАќРЈAМЖКЭBМЖЃЉЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЃКЂйШчЙћ3ЁЂ4ЁЂ5ЮЊвЛзщЙДЙЩЪ§ЃЌФЧУД3kЁЂ4kЁЂ5kШдЪЧЙДЙЩЪ§ЃЛЂкКЌга45ЁуНЧЕФжБНЧШ§НЧаЮЕФШ§БпГЄжЎБШЪЧ1ЁУ1:![]() ЃЛЂлШчЙћвЛИіШ§НЧаЮЕФШ§БпЪЧ9ЃЌ12ЃЌ13ЃЌФЧУДДЫШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЛЂмвЛИіжБНЧШ§НЧаЮЕФСНБпГЄЪЧ3КЭ4ЃЌЫќЕФаББпЪЧ5ЃЎЦфжае§ШЗЕФИіЪ§ЪЧ ( )
ЃЛЂлШчЙћвЛИіШ§НЧаЮЕФШ§БпЪЧ9ЃЌ12ЃЌ13ЃЌФЧУДДЫШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЛЂмвЛИіжБНЧШ§НЧаЮЕФСНБпГЄЪЧ3КЭ4ЃЌЫќЕФаББпЪЧ5ЃЎЦфжае§ШЗЕФИіЪ§ЪЧ ( )
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯB=60ЁуЃЌЖдНЧЯпACЦНЗжНЧЁЯBADЃЌЕуPЪЧЁїABCФквЛЕуЃЌСЌНгPAЁЂPBЁЂPCЃЌШєPA=6ЃЌPB=8ЃЌPC=10ЃЌдђСтаЮABCDЕФУцЛ§ЕШгк_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈxЉ3ЃЉЃЈxЉ4ЃЉЉm2=0ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЖдШЮвтЪЕЪ§mЃЌЗНГЬзмга2ИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШєЗНГЬЕФвЛИіИљЪЧ2ЃЌЧѓmЕФжЕМАЗНГЬЕФСэвЛИіИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌABЃНACЃЌADЃНAEЃЌBEгыCDЯрНЛгкЕуPЃЎ

ЃЈ1ЃЉЧѓжЄЃКPCЃНPBЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁЯCAPЃНЁЯBAPЃЛ
ЃЈ3ЃЉРћгУЃЈ2ЃЉЕФНсТлЃЌгУжБГпКЭдВЙцзїЁЯMONЕФЦНЗжЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
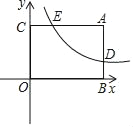
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊОиаЮABOCжаЃЌAC=4ЃЌЫЋЧњЯпy=![]() гыОиаЮСНБпABЁЂACЗжБ№НЛгкDЁЂEЃЌEЮЊACБпжаЕуЃЎ
гыОиаЮСНБпABЁЂACЗжБ№НЛгкDЁЂEЃЌEЮЊACБпжаЕуЃЎ
ЃЈ1ЃЉЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉЕуPЪЧЯпЖЮOBЩЯЕФвЛИіЖЏЕуЃЌЪЧЗёДцдкЕуPЃЌЪЙЁЯDPC=90ЁуЃПШєДцдкЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌABЃНACЃЌЕуDЮЊЁїABCЭтвЛЕуЃЌDCгыABНЛгкЕуOЃЌЧвЁЯBDCЃНЁЯBACЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁЯABDЃНЁЯACDЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAMЁЭCDгкMЃЌЧѓжЄЃКBD+DMЃНCMЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com