
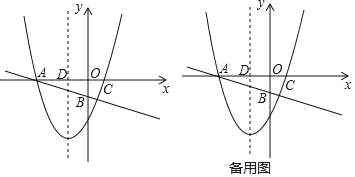
【题目】如图,在直角坐标系中,直线y=﹣![]() x﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
x﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
(1)求抛物线的解析式;
(2)在线段AB上是否存在一点P,使以A,D,P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;如果不存在,请说明理由;
(3)若点Q在第三象限内,且tan∠AQD=2,线段CQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.
【答案】(1)y=x2+2x﹣3;(2)存在;点P坐标为(﹣1,![]() )或(-
)或(-![]() ,-
,-![]() );
);
(3)存在,CQ最小值为![]() .
.
【解析】
(1)根据直线y=﹣![]() x﹣1易求得A点坐标,由抛物线的对称性可求得C点坐标,然后写出抛物线的交点式即可;
x﹣1易求得A点坐标,由抛物线的对称性可求得C点坐标,然后写出抛物线的交点式即可;
(2)根据题意可设点P的坐标为(a,﹣![]() a﹣1),分△AOB∽△APD和△AOB∽△APD两种情况,第一种情况直接根据相似三角形对应边成比例即可求得结果,第二种情况先过点P作PE⊥x轴于点E,则△APE∽△PED,再根据相似三角形对应边成比例即可求得结果;
a﹣1),分△AOB∽△APD和△AOB∽△APD两种情况,第一种情况直接根据相似三角形对应边成比例即可求得结果,第二种情况先过点P作PE⊥x轴于点E,则△APE∽△PED,再根据相似三角形对应边成比例即可求得结果;
(3)如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,﹣![]() )为圆心,因为tan∠AFD=2,
)为圆心,因为tan∠AFD=2,
则连CE交⊙E于点Q,则CQ为满足条件的最小值,再根据两点之间的距离公式求得CE的长,然后减去圆的半径即可得解.
(1)∵直线y=﹣![]() x﹣1与x轴交于A点,
x﹣1与x轴交于A点,
∴点A坐标为(﹣3,0),
又∵直线x=﹣1为对称轴,
∴点C坐标为(1,0),
∴抛物线解析式为:y=(x+3)(x﹣1)=x2+2x﹣3;
(2)存在;
由已知,点D坐标为(﹣1,0),点B坐标为(0,﹣1),
设点P的坐标为(a,﹣![]() a﹣1),
a﹣1),
①当△AOB∽△ADP时,
![]() ,即
,即![]() ,
,
解得:a=﹣1;
点P坐标为(﹣1,![]() );
);
②当△AOB∽△APD时,
过点P作PE⊥x轴于点E,
则△APE∽△PED,
∴PE2=AEED,
∴(﹣![]() a﹣1)2=(a+3)(﹣a﹣1),
a﹣1)2=(a+3)(﹣a﹣1),
解得a1=﹣3(舍去),a2=﹣![]() ,
,
∴点P坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)存在,CQ最小值为![]() ;
;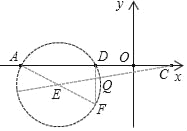
如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,﹣![]() )为圆心,
)为圆心,
∵tan∠AFD=2,
∴弧AFD(A、D除外)上的点都是满足条件的Q点,
则连CE交⊙E于点Q,则CQ为满足条件的最小值,
此时CE=![]() ,
,
∵⊙E半径为![]() ,
,
∴CQ最小值为![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题:①如果3、4、5为一组勾股数,那么3k、4k、5k仍是勾股数;②含有45°角的直角三角形的三边长之比是1∶1:![]() ;③如果一个三角形的三边是9,12,13,那么此三角形是直角三角形;④一个直角三角形的两边长是3和4,它的斜边是5.其中正确的个数是 ( )
;③如果一个三角形的三边是9,12,13,那么此三角形是直角三角形;④一个直角三角形的两边长是3和4,它的斜边是5.其中正确的个数是 ( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
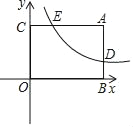
【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=![]() 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.
(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=

A.6 B.8 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为△ABC外一点,DC与AB交于点O,且∠BDC=∠BAC.

(1)求证:∠ABD=∠ACD;
(2)过点A作AM⊥CD于M,求证:BD+DM=CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直角△ABC 中,AC=BC,∠C=90°,∠CAB=∠ABC=45°,过点 B 作射线BD⊥AB 于 B,点 P 为 BC 边上任一点,在射线上取一点 Q,使得 PQ=AP.
(1)请依题意补全图形;
(2)试判断 AP 和 PQ 的位置关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com