
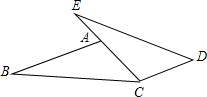
 已知:如图,点E,A,C在同一条直线上,AB=CE,AC=CD,BC=ED.探究AB与CD的位置关系,并证明.
已知:如图,点E,A,C在同一条直线上,AB=CE,AC=CD,BC=ED.探究AB与CD的位置关系,并证明. 科目:初中数学 来源: 题型:解答题
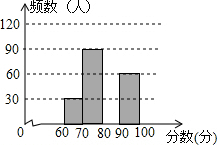 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
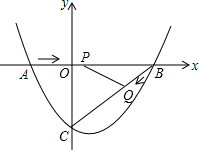 如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
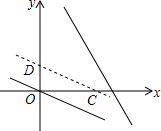 已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点.
已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com