
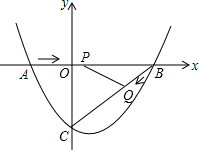
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx-3��a��0����x�ύ�ڵ�A��-2��0����B��4��0�����㣬��y�ύ�ڵ�C��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx-3��a��0����x�ύ�ڵ�A��-2��0����B��4��0�����㣬��y�ύ�ڵ�C������ ��1���ѵ�A��-2��0����B��4��0������������y=ax2+bx-3��a��0�������a��b��c��ֵ���ɣ�
��2�����˶�ʱ��Ϊt�룬��AP=3t��BQ=t��PB=6-3t�����ݹ��ɶ������BC�ij�������Q��QH��AB�ڵ�H����QH��OC�ó���BHQ�ס�BOC���������������εĶ�Ӧ�߳ɱ�����t��ʾ��HQ�ij����������ε������ʽ�ó������ε������t�ĺ�����ϵʽ�����ݶ��κ��������ʼ��ɵó����ۣ�
��3���֡�BPQ=90�����PQB=90����������������ۣ�
��� 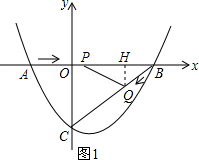 �⣺��1����������y=ax2+bx-3��a��0����x�ύ�ڵ�A��-2��0����B��4��0�����㣬
�⣺��1����������y=ax2+bx-3��a��0����x�ύ�ڵ�A��-2��0����B��4��0�����㣬
��$\left\{\begin{array}{l}4a-2b-3=0\\ 16a+4b-3=0\end{array}\right.$�����$\left\{\begin{array}{l}a=\frac{3}{8}\\ b=-\frac{3}{4}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
��2�����˶�ʱ��Ϊt�룬��AP=3t��BQ=t��PB=6-3t��
���ɣ�1��֪�������ߵĽ���ʽΪy=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
��C��0��-3����
��Rt��OBC��BC=$\sqrt{{OB}^{2}+{OC}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5��
��ͼ1������Q��QH��AB�ڵ�H��
��QH��OC��
���BHQ�ס�BOC��
��$\frac{HQ}{OC}$=$\frac{BQ}{BC}$����$\frac{HQ}{3}$=$\frac{t}{5}$��
��HQ=$\frac{3}{5}$t��
��S��PBQ=$\frac{1}{2}$PB•HQ=$\frac{1}{2}$��6-3t��•$\frac{3}{5}$t=-$\frac{9}{10}$t2+$\frac{9}{5}$t��
�൱t=-$\frac{\frac{9}{5}}{2����-\frac{9}{10}��}$=1ʱ��S���=$\frac{��\frac{9}{5}��^{2}}{4����-\frac{9}{10}��}$=$\frac{9}{10}$��
��3�����ڣ�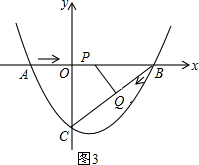
��ͼ2��ʾ������BPQ=90��ʱ����ʱ��BPQ�ס�BOC��
��BQ=t��PB=6-3t��OB=4��OC=3��BC=5��
��$\frac{BP}{OB}$=$\frac{BQ}{BC}$����$\frac{6-3t}{4}$=$\frac{t}{5}$�����t=$\frac{30}{19}$���룩��
��ͼ3��ʾ������PQB=90��ʱ����ʱ��BPQ�ס�BCO��
��BQ=t��PB=6-3t��OB=4��OC=3��BC=5��
��$\frac{BQ}{OB}$=$\frac{BP}{BC}$����$\frac{t}{4}$=$\frac{6-3t}{5}$�����t=$\frac{24}{17}$���룩��
������������t=$\frac{30}{19}$���$\frac{24}{17}$��ʱ���Ե�P��B��Q���ɵ����������BOC���ƣ�
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����κ���ͼ���ϵ�������ص㡢���������ε��ж������ʵ�֪ʶ���ڽ��3��ʱҪע����з������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����3�� | B�� | ��СΪԭ����$\frac{1}{3}$ | C�� | ������ | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
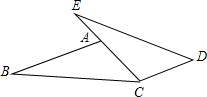 ��֪����ͼ����E��A��C��ͬһ��ֱ���ϣ�AB=CE��AC=CD��BC=ED��̽��AB��CD��λ�ù�ϵ����֤����
��֪����ͼ����E��A��C��ͬһ��ֱ���ϣ�AB=CE��AC=CD��BC=ED��̽��AB��CD��λ�ù�ϵ����֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 4.1 | 4.2 | 4.3 | 4.4 |
| y | -0.69 | -0.36 | -0.01 | 0.35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
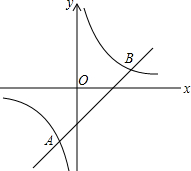 ��ͼ��ʾ��һ�κ���y1=ax+b��ͼ���뷴��������y2=$\frac{3}{x}$��ͼ���ཻ��A��B���㣬��y1��y2ʱ��-1��x��0��x��3����һ�κ����Ľ���ʽΪy=x-2��
��ͼ��ʾ��һ�κ���y1=ax+b��ͼ���뷴��������y2=$\frac{3}{x}$��ͼ���ཻ��A��B���㣬��y1��y2ʱ��-1��x��0��x��3����һ�κ����Ľ���ʽΪy=x-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com