
【题目】(本小题满分10分 )在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况,请跟据小丽提供的信息,解答小华和小明提出的问题
小丽:每个定价3元,每天能卖出500个,而且,这种粽子每上涨0.1元,其售销量将减小10个
小华:照你所说,如果实现每天800元的售销利润,那该如何定价?莫忘了物价局规定售价不能超过进价的240%哟
小明:800元售销利润是不是最多的呢?如果不是,那该如何定价,才会使每天的利润最大?.
(1)小华的问题解答:
(2)小明的问题解答:
【答案】(1)当定价为4元时,能实现每天800元的销售利润;(2)800元的销售利润不是最多,当定价为4.8元时,每天的销售利润最大
【解析】
试题(1)设定价为x元,利润为y元,由题意得,y=(x-2)(500-![]() ×10)
×10)
y=-100(x-5)2+900, -100(x-5)2+900,=800,解得:x=4或x=6,
∵售价不能超过进价的240%,∴x≤2×240%,即x≤4.8,故x=4,
即小华问题的解答为:当定价为4元时,能实现每天800元的销售利润;
(2)由(1)得y=-100(x-5)2+900,
∵-100<0,∴函数图象开口向下,且对称轴为直线x=5,
∵x≤4.8,故当x=4.8时函数能取最大值,
即y最大=-100(x-5)2+900=896.
故小明的问题的解答为:800元的销售利润不是最多,当定价为4.8元时,每天的销售利润最大.
考点: 二次函数的应用


科目:初中数学 来源: 题型:
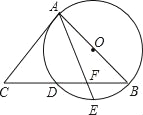
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
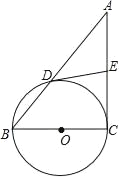
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
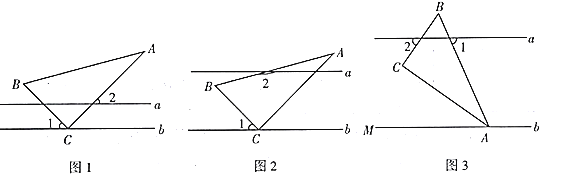
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
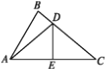
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
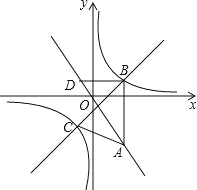
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
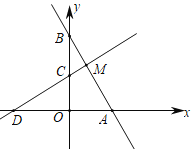
【题目】如图,直线l1:y=﹣2x+2交x轴于点A,交y轴于点B,直线l2:y=![]() x+1交x轴于点D,交y轴于点C,直线l1、l2交于点M.
x+1交x轴于点D,交y轴于点C,直线l1、l2交于点M.
(1)点M坐标为_____;
(2)若点E在y轴上,且△BME是以BM为一腰的等腰三角形,则E点坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com