
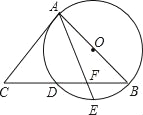
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
【答案】(1)证明见解析;(2) ①BC=9;②DF=2.
【解析】
(1) 连结AD, 根据圆周角定理,由E是BD的中点得到∠EAB=∠EAD, 由于∠ACB=2∠EAB, 则∠ACB=∠DAB, 再利用圆周角定理得到∠ADB=![]() , 则∠DAC+∠ACB=90, 所以∠DAC+∠DAB=
, 则∠DAC+∠ACB=90, 所以∠DAC+∠DAB=![]() , 于是根据切线的判定定理得到AC是OO的切线;
, 于是根据切线的判定定理得到AC是OO的切线;
(2)①在Rt△ABC中, 根据cosC=![]() =
=![]() =
=![]() ,AC=6可得AC=6;
,AC=6可得AC=6;
②作FH⊥AB于H, 由BD=BC-CD=5, ∠EAB=∠EAD, FD⊥AD,FH⊥AB, 推出FD=FH, 设FB=x, 则DF=FH=5-x, 根据cos∠BFH=cos∠C=![]() =
=![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(1)连结AD,如图,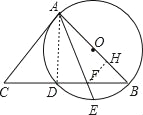
∵E是![]() 的中点,
的中点,
∴![]() =
=![]() =,
=,
∴∠EAB=∠EAD,
∵∠ACB=2∠EAB,
∴∠ACB=∠DAB,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAC+∠ACB=90°,
∴∠DAC+∠DAB=90°,即∠BAC=90°,
∴AC⊥AB,
∴AC是⊙O的切线;
(2)①在Rt△ACB中,
∵cosC=![]() =
=![]() =
=![]() ,AC=6,
,AC=6,
∴BC=9.
②作FH⊥AB于H,
∵BD=BC﹣CD=5,∠EAB=∠EAD,FD⊥AD,FH⊥AB,
∴FD=FH,设FB=x,则DF=FH=5﹣x,
∵FH∥AC,
∴∠HFB=∠C,
在Rt△BFH中,
∵cos∠BFH=cos∠C=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=3,即BF的长为3,
∴DF=2


科目:初中数学 来源: 题型:
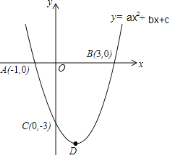
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 抛物线的对称轴上是否存在一点
抛物线的对称轴上是否存在一点![]() ,使
,使![]() 为等腰三角形?若存在,写出点
为等腰三角形?若存在,写出点![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
![]() 点
点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() ,求四边形
,求四边形![]() 面积的最大值,以及此时点
面积的最大值,以及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
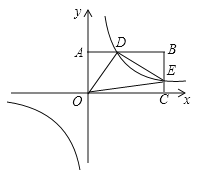
(1)①点B的坐标为 ;②S S(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
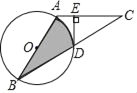
【题目】如图,AB是⊙O的直径,C是⊙O外一点,AB=AC,连接BC,交⊙O于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE与⊙O相切.
(2)若∠B=30°,AB=4,则图中阴影部分的面积是 (结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
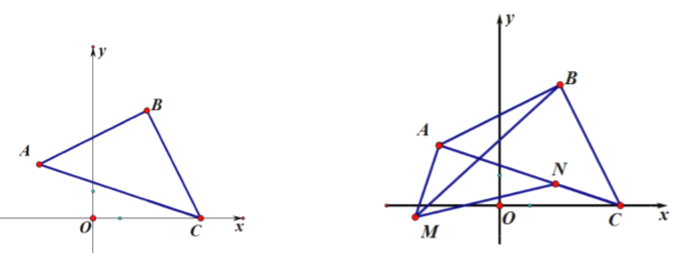
【题目】如图,直线y=﹣x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分 )在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况,请跟据小丽提供的信息,解答小华和小明提出的问题
小丽:每个定价3元,每天能卖出500个,而且,这种粽子每上涨0.1元,其售销量将减小10个
小华:照你所说,如果实现每天800元的售销利润,那该如何定价?莫忘了物价局规定售价不能超过进价的240%哟
小明:800元售销利润是不是最多的呢?如果不是,那该如何定价,才会使每天的利润最大?.
(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,且
,且 ![]() ,
,![]() 满足
满足![]() .
.
(1)写出![]() 、
、![]() 两点坐标;
两点坐标;
(2)求![]() 点坐标;
点坐标;
(3)如图,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,请写出线段
,请写出线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com