
| A. | x=1 | B. | x=-1 | C. | x=5 | D. | x=-5 |
分析 作为反例,要满足条件但不能得到结论,然后根据这个要求对各选项进行判断.
解答 解:当x=1,-5时,(x+1)( x-5 )=0不成立,即不满足条件;
当x=-1时,(x+1)( x-5 )=0成立,满足条件,但是也满足结论;
当x=5时,(x+1)( x-5 )=0成立,满足条件,不满足结论,所以证明命题“若(x+1)( x-5 )=0,则x=-1”是假命题的反例是:x=5.
故选C.
点评 本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题.命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | ${({\frac{{2{x^2}}}{2y}})^3}=\frac{{2{x^6}}}{{2{y^3}}}$ | B. | ${({\frac{2a}{a+b}})^2}=\frac{{4{a^2}}}{{{a^2}+{b^2}}}$ | ||
| C. | ${({\frac{m+n}{m-n}})^3}=\frac{{{{(m+n)}^3}}}{{{{(m-n)}^3}}}$ | D. | ${({\frac{x-y}{x+y}})^2}=\frac{{{x^2}-{y^2}}}{{{x^2}+{y^2}}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 82° | B. | 53° | C. | 45° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
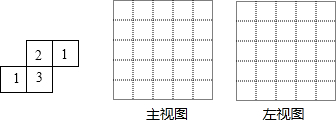
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com