
 一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象交于A(-2,b)、B两点.若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,则m的值为( )
一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象交于A(-2,b)、B两点.若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,则m的值为( )| A. | 1 | B. | 1或8 | C. | 2或8 | D. | 1或9 |
分析 先利用反比例函数解析式求出b,得到A点坐标为(-2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式;由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y=kx+5-m,则直线y=kx+5-m与反比例函数有且只有一个公共点,即方程组,只有一组解,然后消去y得到关于x的二次函数,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
解答 解:把A(-2,b)代入y=-$\frac{8}{x}$得b=-$\frac{8}{-2}$=4,
所以A点坐标为(-2,4),
把A(-2,4)代入y=kx+5得-2k+5=4,解得k=$\frac{1}{2}$,
所以一次函数解析式为y=$\frac{1}{2}$x+5;
将直线AB向下平移m(m>0)个单位长度得直线解析式为y=$\frac{1}{2}$x+5-m,
根据题意方程组$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=\frac{1}{2}x+5-m}\end{array}\right.$只有一组解,
消去y得-$\frac{8}{x}$=$\frac{1}{2}$x+5-m,
整理得$\frac{1}{2}$x2-(m-5)x+8=0,
△=(m-5)2-4×$\frac{1}{2}$×8=0,解得m=9或m=1,
故选D.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了一次函数与几何变换.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是⊙O的直径,以AD为边作平行四边形ABCD,AB与⊙O交于点F,在边
如图,AD是⊙O的直径,以AD为边作平行四边形ABCD,AB与⊙O交于点F,在边查看答案和解析>>
科目:初中数学 来源: 题型:解答题
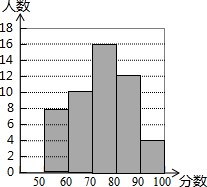 本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)用5块正方体的木块搭出如图所示的图形,画出它从正面、左面、上面三个方向看到的图形.
(1)用5块正方体的木块搭出如图所示的图形,画出它从正面、左面、上面三个方向看到的图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B=30°,ED垂直平分BC,若BC=6,则BE=( )
如图,在△ABC中,∠B=30°,ED垂直平分BC,若BC=6,则BE=( )| A. | 2$\sqrt{3}$ | B. | 3 | C. | $\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,O是直线AB上的一点,∠BOC=120°,OD平分∠AOC.0E平分∠BOC,则图中与∠BOE互余的角有( )
如图,O是直线AB上的一点,∠BOC=120°,OD平分∠AOC.0E平分∠BOC,则图中与∠BOE互余的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com