
【题目】如图,在下面直角坐标系中,已知![]()

(1)求![]() 的面积
的面积
(2)若以点![]() 为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点
为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点![]() 的坐标
的坐标
(3)是否存在![]() 轴上的点
轴上的点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,若存在,求出点
倍,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)16;(2)(4,4)或(12,4)或(4,4);(3) 存在,点M的坐标为(24,0)或(8,0).
【解析】
(1)由A点坐标得到△ABO边OB上的高为|-4|,则可根据三角形面积公式计算△ABO的面积;
(2)用图形平移的特性:线段上的点坐标变化是一样的得出C点的坐标;
(3)M点在x轴上,那么![]() 和
和![]() 是登高的,只要找出底BM是OB的两倍的点M就行.
是登高的,只要找出底BM是OB的两倍的点M就行.
(1)![]() ;
;
(2) 以点![]() 为顶点画平行四边形,当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位,得到C的坐标(4,4);当把OA向左平移8个单位,即把点A(-4,-4)向左平移8个单位得到C的坐标(-12,4);当把AB向上平移A移到O,xy轴坐标都增加了4,B的坐标也得增加4,得到C的坐标(-4,4),
为顶点画平行四边形,当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位,得到C的坐标(4,4);当把OA向左平移8个单位,即把点A(-4,-4)向左平移8个单位得到C的坐标(-12,4);当把AB向上平移A移到O,xy轴坐标都增加了4,B的坐标也得增加4,得到C的坐标(-4,4),
∴C的坐标为(4,4)或(12,4)或(4,4);
(3)存在.
![]() ×|x+8|×4=2
×|x+8|×4=2![]() =32,解得x=8或24,
=32,解得x=8或24,
∴点M的坐标为(24,0)或(8,0).


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )
A. 290×![]() B. 290×
B. 290×![]()
C. 2.90×![]() D. 2.90×
D. 2.90×![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
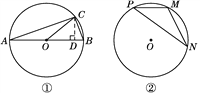
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=![]() ,求sin 2α的值.
,求sin 2α的值.
小娟是这样给小芸讲解的:
如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=![]() =
=![]() .易得∠BOC=2α.设BC=x,则AB=3x,AC=2
.易得∠BOC=2α.设BC=x,则AB=3x,AC=2![]() x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=
x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=![]() =________.
=________.
【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=![]() ,求sin 2β的值.
,求sin 2β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
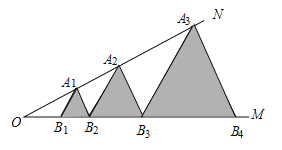
【题目】如图已知:![]() 点
点![]() ···,在射线
···,在射线![]() 上,点
上,点![]() ,···,在射线
,···,在射线![]() 上,
上,![]() ,···,均为等边三角形,若
,···,均为等边三角形,若![]() 则
则![]() 的边长为________________________.
的边长为________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com