

���� ��1�����ݴ�ֱ�Ķ���õ���AOC=��BOC=90�㣬���ݽ�ƽ���ߵĶ��弴�ɵõ����ۣ�
��2�����ݽ�ƽ���ߵĶ���õ���EOD=$\frac{1}{2}$��AOD=$\frac{1}{2}$����80+�£�=40+$\frac{1}{2}$�£���COF=$\frac{1}{2}$��BOC=$\frac{1}{2}$����80+�£�=40+$\frac{1}{2}$�£����ݽǵĺͲ�ɵõ����ۣ�
��3����ͼ2����֪�����õ���AOD=��+�£����ݽ�ƽ���ߵĶ���õ���DOE=$\frac{1}{2}$����+�£������ɵõ����ۣ�
��� �⣺��1����CO��AB��
���AOC=��BOC=90�㣬
��OEƽ�֡�AOC��
���EOC=$\frac{1}{2}$��AOC=$\frac{1}{2}$��90��=45�㣬
��OFƽ�֡�BOC��
���COF=$\frac{1}{2}$��BOC=$\frac{1}{2}$��90��=45�㣬
��EOF=��EOC+��COF=45��+45��=90�㣻
��2����OEƽ�֡�AOD��
���EOD=$\frac{1}{2}$��AOD=$\frac{1}{2}$����80+�£�=40+$\frac{1}{2}$�£�
��OFƽ�֡�BOC��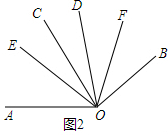
���COF=$\frac{1}{2}$��BOC=$\frac{1}{2}$����80+�£�=40+$\frac{1}{2}$�£�
��COE=��EOD-��COD=40+$\frac{1}{2}$ ��-��=40-$\frac{1}{2}$�£�
��EOF=��COE+��COF=40-$\frac{1}{2}$ ��+40+$\frac{1}{2}$��=80�㣻
��3����ͼ2���ߡ�AOC=��BOD=������COD=�£�
���AOD=��+�£�
��OEƽ�֡�AOD��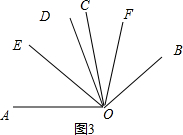
���DOE=$\frac{1}{2}$����+�£���
���COE=��DOE-��COD=$\frac{1}{2}����+�£�-��$=$\frac{1}{2}��-\frac{1}{2}��$��
��ͼ3���ߡ�AOC=��BOD=������COD=�£�
���AOD=��+�£�
��OEƽ�֡�AOD��
���DOE=$\frac{1}{2}$����-�£���
���COE=��DOE+��COD=$\frac{1}{2}��+\frac{1}{2}��$��
����������$\frac{1}{2}����\frac{1}{2}��$��
�ʴ�Ϊ��$\frac{1}{2}����\frac{1}{2}��$��
���� ���⿼���˽�ƽ���ߵĶ��壬�ǵļ��㣬����Ĺؼ����ҳ����еĵ�����ϵ�з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 һ�����dz�ƴ����ͼ��ʾ��ͼ�������ABC�Ĵ�СΪ��������
һ�����dz�ƴ����ͼ��ʾ��ͼ�������ABC�Ĵ�СΪ��������| A�� | 100�� | B�� | 110�� | C�� | 120�� | D�� | 135�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
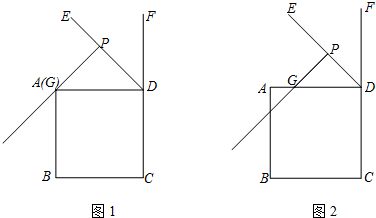
 ��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E����ABC�����Ϊ20��AB=12��BC=8����DE�ij�Ϊ2��
��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E����ABC�����Ϊ20��AB=12��BC=8����DE�ij�Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com