
 如图所示,两根旗杆间相距12m,某人从C点沿CA走向A,一定时间后他到达点B,此时他仰望旗杆的顶点E和D,两次视线的夹角为90°,且EB=BD,已知旗杆AE的高为8m,该人的运动速度为1m/s,则这个人运动了
如图所示,两根旗杆间相距12m,某人从C点沿CA走向A,一定时间后他到达点B,此时他仰望旗杆的顶点E和D,两次视线的夹角为90°,且EB=BD,已知旗杆AE的高为8m,该人的运动速度为1m/s,则这个人运动了
|


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
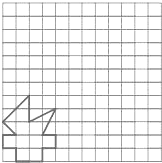 为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.
为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.查看答案和解析>>
科目:初中数学 来源: 题型:
| AB |
| AC |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| A、20 | B、18 | C、16 | D、9 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
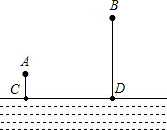 如图,A、B两个化工厂在河道CD的同侧,A、B两厂到河的距离分别为AC=2km,BD=3km,CD=12km,现在河边CD上建污水处理站,将A、B两厂输送的污水处理后再排入河道,设铺设排污水管的费用为20000元/千米,请你在河道CD边上选择污水站位置O,使铺设排污水管的费用最省,并求出铺设排污水管的总费用?
如图,A、B两个化工厂在河道CD的同侧,A、B两厂到河的距离分别为AC=2km,BD=3km,CD=12km,现在河边CD上建污水处理站,将A、B两厂输送的污水处理后再排入河道,设铺设排污水管的费用为20000元/千米,请你在河道CD边上选择污水站位置O,使铺设排污水管的费用最省,并求出铺设排污水管的总费用?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
| 甲组 | 7 | 7 | 7 | ||
| 乙组 | 2.6 | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com