
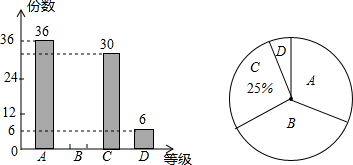
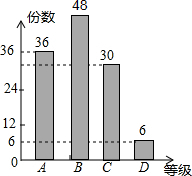
| 6 |
| 120 |
|


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
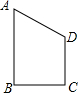 四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线
四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,两根旗杆间相距12m,某人从C点沿CA走向A,一定时间后他到达点B,此时他仰望旗杆的顶点E和D,两次视线的夹角为90°,且EB=BD,已知旗杆AE的高为8m,该人的运动速度为1m/s,则这个人运动了
如图所示,两根旗杆间相距12m,某人从C点沿CA走向A,一定时间后他到达点B,此时他仰望旗杆的顶点E和D,两次视线的夹角为90°,且EB=BD,已知旗杆AE的高为8m,该人的运动速度为1m/s,则这个人运动了查看答案和解析>>
科目:初中数学 来源: 题型:
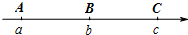 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB=BC,如果点A到原点的距离最大,点B到原点的距离最小,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB=BC,如果点A到原点的距离最大,点B到原点的距离最小,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点C的右边 |
查看答案和解析>>
科目:初中数学 来源: 题型:
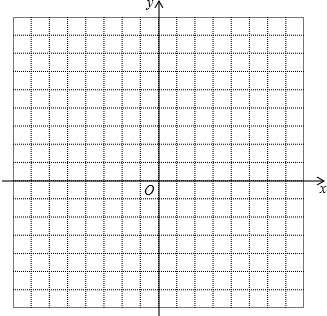 已知二次函数y=
已知二次函数y=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com