
 ��ͼ����֪������y=x2+bx+c��һֱ���ཻ��A��-1��0����C��2��-3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��ͼ����֪������y=x2+bx+c��һֱ���ཻ��A��-1��0����C��2��-3�����㣬��y�ύ�ڵ�N���䶥��ΪD������ ��1�����ô���ϵ��������κ�������ʽ��һ�κ�������ʽ��
��2����������֮���߶������N�����ֱ��x=3�ĶԳƵ�N�䣬��M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��3����Ҫ�������ۣ��ٵ���E���߶�AC��ʱ����F�ڵ�E�Ϸ�����F��x��x+3���͢ڵ���E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�����F��x��x-1����Ȼ�����ö��κ���ͼ���ϵ����������������õ�E�����ꣻ
��4������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G����ͼ1����Q��x��x+1������P��x��-x2+2x+3�������������ľ��빫ʽ��������߶�PQ=-x2+x+2�������ͼʾ�Լ������ε������ʽ�������̼��ɣ�
��� �⣺��1����������y=-x2+bx+c����A��-1��0����C��2��3���ã�
$\left\{\begin{array}{l}{-1+b+c=0}\\{-4+2b+c=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��
��������Ϊy=-x2+2x+3
����ֱ��Ϊy=kx+n����A��-1��0����C��2��3����$\left\{\begin{array}{l}{-k+n=0}\\{2k+n=3}\end{array}\right.$
���$\left\{\begin{array}{l}{k=1}\\{n=1}\end{array}\right.$��
��ֱ��ACΪy=x+1��ֱ��ACΪy=x+1��
��2����ͼ1����N�����ֱ��x=3�ĶԳƵ�N�䣬��N�䣨6��3�����ɣ�1����D��1��4����
��ֱ��DN��ĺ�����ϵʽΪy=-$\frac{1}{5}$x+$\frac{21}{5}$��
��M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��m=-$\frac{1}{5}$��3+$\frac{21}{5}$=$\frac{18}{5}$��
��3���ɣ�1������2����D��1��4����B��1��2����
�ߵ�E��ֱ��AC�ϣ�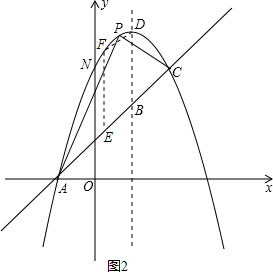
��E��x��x+1����
����ͼ2������E���߶�AC��ʱ����F�ڵ�E�Ϸ���
��F��x��x+3����
��F���������ϣ�
��x+3=-x2+2x+3��
��ã�x=0��x=1����ȥ��
��E��0��1����
�ڵ���E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·���
��F��x��x-1��
��F����������
��x-1=-x2+2x+3
���x=$\frac{1-\sqrt{17}}{2}$��x=$\frac{1+\sqrt{17}}{2}$��
��E��$\frac{1-\sqrt{17}}{2}$��$\frac{3-\sqrt{17}}{2}$����$\frac{1+\sqrt{17}}{2}$��$\frac{3+\sqrt{17}}{2}$��
���ϣ����������ĵ�E������Ϊ��0��1����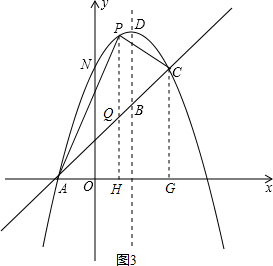 ��$\frac{1-\sqrt{17}}{2}$��$\frac{3-\sqrt{17}}{2}$����$\frac{1+\sqrt{17}}{2}$��$\frac{3+\sqrt{17}}{2}$��
��$\frac{1-\sqrt{17}}{2}$��$\frac{3-\sqrt{17}}{2}$����$\frac{1+\sqrt{17}}{2}$��$\frac{3+\sqrt{17}}{2}$��
��4����ͼ3������P��PQ��x�ύAC�ڵ�Q����x���ڵ�H������C��CG��x���ڵ�G����Q��x��x+1������P��x��-x2+2x+3��
��PQ=��-x2+2x+3��-��x+1��
=-x2+x+2
�֡�S��APC=S��APQ+S��CPQ
=$\frac{1}{2}$PQ•AG
=$\frac{1}{2}$��-x2+x+2����3
�ߡ�APC�����Ϊ3��
��$\frac{1}{2}$��-x2+x+2����3=3
��x=-1��x=2��
��P��-1��0����2��3����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������ͼ�ε�����������ļ�ֵ�����3����ʱ��Ҫ�Ե�E���ڵ�λ�ý��з������ۣ��Է�©�⣮


 �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
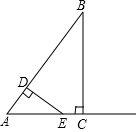 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=3��BC=4������D�ӵ�A������ÿ��3����λ���ٶ��˶�����B������D��DE��AB������AC�ڵ�E�����D���˶�ʱ��Ϊt�루t��0����
��ͼ����Rt��ABC�У���ACB=90�㣬AC=3��BC=4������D�ӵ�A������ÿ��3����λ���ٶ��˶�����B������D��DE��AB������AC�ڵ�E�����D���˶�ʱ��Ϊt�루t��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
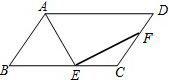 ��ͼ��ƽ���ı���ABCD�У�AEƽ�֡�BAD��BC����E��EF��AE��CD����F��EC=CF����BC=7��DF=3��tan��AEB=3����ƽ���ı���ABCD�����Ϊ21��
��ͼ��ƽ���ı���ABCD�У�AEƽ�֡�BAD��BC����E��EF��AE��CD����F��EC=CF����BC=7��DF=3��tan��AEB=3����ƽ���ı���ABCD�����Ϊ21���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | �� | -1 | 0 | 1 | 2 | �� |
| y | �� | 0 | 3 | 4 | 3 | �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com