

分析 (1)延长BM交DA延长线于点G,根据已知条件得到ADE=$\frac{1}{2}$∠ABC=45°,求得∠ABC=90°,推出DA∥BC,根据平行线的性质得到∠ADM=∠BCM,推出△DAM≌△CBM,于是得到DG=BC=AB,BM=GM,求出AG=BE,证得△ABG≌△BCE,根据全等三角形的性质得到BG=CE,等量代换即可得到结论;
(2)过点B作BG⊥AC于点G,连接MG,根据已知条件得到MG=$\frac{1}{2}$AD,MG∥AD,由平行线的性质得到∠MGC=∠DAC,求得tanα=$\frac{AE}{AD}$=$\frac{AG}{BG}$,求得$\frac{AE}{GM}=\frac{AC}{BG}$,推出∠EAC=∠BGM,证得△ACE∽△BMG,根据相似三角形的性质即可得到结论.
解答 解:(1)BM=$\frac{1}{2}$CE;
延长BM交DA延长线于点G,
∵AE⊥AD,
∴∠DAE=90°,
∵∠ADE=$\frac{1}{2}$∠ABC=45°,
∴∠ABC=90°,
∴DA∥BC,
∴∠ADM=∠BCM,
在△DAM与△CBM中,
$\left\{\begin{array}{l}{∠GDM=∠BCM}\\{∠DMG=∠BMC}\\{DM=CM}\end{array}\right.$,
∴△DGM≌△CBM,
∴DG=BC=AB,BM=GM,
∵AD=AE,
∴AG=BE,
在△ABG与△BCE中,
$\left\{\begin{array}{l}{AG=BE}\\{∠GAB=∠EBC=90°}\\{AB=BC}\end{array}\right.$,
∴△ABG≌△BCE,
∴BG=CE,
∴BM=$\frac{1}{2}$CE;
(2)过点B作BG⊥AC于点G,连接MG,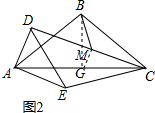 ∵AB=BC,
∵AB=BC,
∴$∠ABG=\frac{1}{2}∠ABC=∠ADE=α$,AG=CG,
∵DM=CM,
∴MG=$\frac{1}{2}$AD,MG∥AD,
∴∠MGC=∠DAC,
∵tanα=$\frac{AE}{AD}$=$\frac{AG}{BG}$,
∴$\frac{AE}{2GM}=\frac{\frac{1}{2}AC}{BG}$,
∴$\frac{AE}{GM}=\frac{AC}{BG}$,
∵∠DAC+∠CAE=∠BGM+∠MGC=90°,
∴∠EAC=∠BGM,
∴△ACE∽△BMG,
∴$\frac{BM}{CE}$=$\frac{AE}{MG}$=$\frac{AE}{\frac{1}{2}AD}$=1:2tanα.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,等腰三角形的性质,三角形的中位线的性质,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
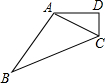 如图,在四边形ABCD中,CA平分∠DCB,∠ADC=∠BAC=90°.
如图,在四边形ABCD中,CA平分∠DCB,∠ADC=∠BAC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
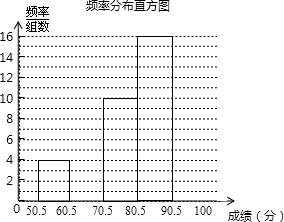 6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{300}{1.2x}$$\frac{300}{x}$=2 | B. | $\frac{300}{x}$-$\frac{300}{1.2x}$=2 | C. | $\frac{300}{1.2x}$=$\frac{300}{x-2}$ | D. | $\frac{300}{x+2}$=$\frac{300}{1.2x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com