
【题目】请阅读下列材料:
提出问题:现有2个边长是1的小正方形,请你把它们分割后,(图形不得重叠,不得遗漏),组成一个大的正方形,解决这个问题的方法不唯一,但有一个解题的思路是:设新正方形的边长为![]() .依题意,割补前后图形的面积相等,有
.依题意,割补前后图形的面积相等,有![]() ,解得
,解得![]() ,由此可知新正方形的边长等于原来正方形的对角线的长.
,由此可知新正方形的边长等于原来正方形的对角线的长.
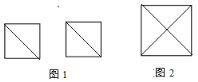
(1)解决问题:现有5个边长为1的正方形,排列形式如图3,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
小东同学的做法是:设新正方形的边长为![]() (
(![]() ).依题意,割补前后图形的面积相等,有 ,解得
).依题意,割补前后图形的面积相等,有 ,解得![]() = .由此可知新正方形的边长等于两个正方形组成的矩形对角线的长.请你在图3中画出分割线,在图4中拼出新的正方形.
= .由此可知新正方形的边长等于两个正方形组成的矩形对角线的长.请你在图3中画出分割线,在图4中拼出新的正方形.
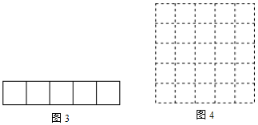
(2)模仿演练:
现有10个边长为1的正方形,排列形式如图5,请把它们分割后拼接成一个新的正方形.要求:在图5中画出分割线,并在图6中的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.说明:直接画出图形,不要求写分析过程.

(3)应用创新:
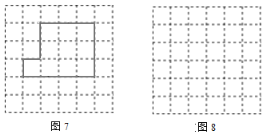
图7是一个大的矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图7中画出分割线,在图8中要求画出三块图形组装成大正方形的示意图).
科目:初中数学 来源: 题型:
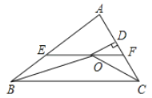
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,下列四个结论:
,下列四个结论:
①![]() ;②
;②![]() ;
;
③点![]() 到
到![]() 各边的距离相等;③设
各边的距离相等;③设![]() ,
,![]() ,则
,则![]() .
.
其中正确的结论是__________.(填所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
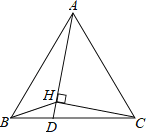
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
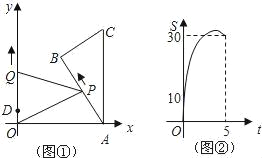
【题目】如图①,Rt△ABC中,∠B=90°∠CAB=30°,AC⊥x轴.它的顶点A的坐标为(10,0),顶点B的坐标为(5,5![]() ),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)求∠BAO的度数.(直接写出结果)
(2)当点P在AB上运动时,△OPQ的面积S与时间t(秒)之间的函数图象为抛物线的一部分(如图②),求点P的运动速度.
(3)求题(2)中面积S与时间t之间的函数关系式,及面积S取最大值时,点P的坐标.
(4)如果点P,Q保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
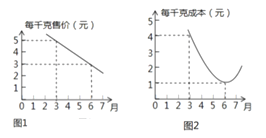
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为CD上一点,连接BE, ∠EBC=15°,将ΔEBC绕点C按顺时针方向旋转90°得到ΔFDC,连接EF,则∠EFD的度数为( )

A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com