练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
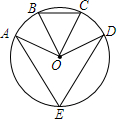
    18．如图，已知点E是⊙O上的点，B、C分别是劣弧AD的三等分点，∠BOC=46°，则∠AED=（　　）
    A．46°B．68°C．69°D．70°

    分析 先根据圆心角、弧、弦的关系求出∠AOD的度数，再由圆周角定理得出∠AED的度数即可．

    解答 解：∵点E是圆O上的点，B、C分别是劣弧AD的三等分点，∠BOC=46°，
    ∴∠AOD=3∠BOC=3×46°=138°，
    ∴∠AED=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×138°=69°，
    故选C．

    点评 本题考查的是圆周角定理，即在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．计算：（1）3-4=-1；（2）-2+5=3；（3）$（-6）×（\frac{1}{2}-\frac{1}{3}）$=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，△ABC中，BD平分∠ABC，∠ABC=60°，∠C=40°，求∠ADB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．当n=1，2，3，4，5，…，2012，2013时，二次函数y=（n2+n）x2-（2n+1）x+1的图象与x轴所截的线段长度之和为（　　）
    A．$\frac{2011}{2012}$B．$\frac{2012}{2013}$C．$\frac{2013}{2014}$D．$\frac{2014}{2015}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．南昌市某路公交车共有10站，我们把上客人数记为“+”，把下客人数记为“-”，一次该路一辆公交车各站上、下人数列表如下：
     ①始发站 ② ③ ④ ⑤ ⑥ ⑦⑧ ⑨ ⑩终点站
     上客人数 9 8 10 121413 11 6 7 0
     下客人数0 -3-5 -7-4-8-6-9 x-28
    （1）求表格中x的值；
    （2）求在⑤、⑥站之间该公交车上的人数；
    （3）问在哪两站之间，该公交车上的人数最多？并求最多人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

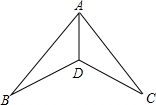    3．如图，下列条件中，不能证明△ABD≌△ACD的是（　　）
    A．∠B=∠C，BD=DCB．BD=DC，AB=ACC．∠B=∠C，∠BAD=∠CADD．∠ADB=∠ADC，BD=DC

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知直角三角形的两条直角边长分别为6cm和8cm，则斜边上的高为4.8cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，点D在边BC上，AD=BD=AC，∠BAC=72°，则∠DAC=36°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

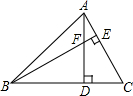    8．如图，△ABC中，∠ABC=45°，高AD、BE相交于点F，CD=4，则线段DF的长为（　　）
    A．2$\sqrt{2}$B．4C．3$\sqrt{2}$D．4$\sqrt{2}$

    查看答案和解析>>

    同步练习册答案