
【题目】如图1所示,在![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,点
,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,
,![]() 满是条件
满是条件![]() .
.

(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)求证:![]() ;
;
(3)如图2,点![]() 是线段
是线段![]() 延长线上一点,其余条件与题干一致,探究
延长线上一点,其余条件与题干一致,探究![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
【答案】(1)AB=4;(2)见详解;(3)AE+AF=BC,证明见详解.
【解析】
(1)在等腰直角三角形DEF中,∠DEF=90°,求得∠1=20°,根据余角的定义得到∠2=∠DEF-∠1=70°,根据三角形的内角和得到∠3=60°,∠4=30°根据三角函数的定义得到AB=2BC,于是得到结论;
(2)如图1,过D作DM⊥AE于D,在△DEM中,由余角的定义得到∠2+∠5=90°,由于∠2+∠1=90°,推出∠1=∠5证得△DEM≌△EFA,根据全等三角形的性质得到AF=EM,根据三角形的内角和和余角的定义得到∠3=∠B,推出△DAM≌△ABC,根据全等三角形的性质得到BC=AM,即可得到结论;
(3)如图2,过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B,证得△ADM≌△BAC,由全等三角形的性质得到BC=AM,由于EF=DE,∠DEF=90°,推出∠4=∠5,证得△MED≌△AFE,根据全等三角形的性质得到ME=AF,即可得到结论.
解:(1)在等腰直角三角形DEF中,∠DEF=90°,

∵∠1=20°,
∴∠2=∠DEF![]() ∠1=70°,
∠1=70°,
∵∠EDA+∠2+∠3=180°,
∴∠3=60°,
∵EA⊥AB,
∴∠EAB=90°,
∵∠3+∠EAB+∠4=180°,
∴∠4=30°,
∵∠C=90°,
∴AB=2BC=4;
(2)如图1,过D作DM⊥AE于M,

在△DEM中,∠2+∠5=90°,
∵∠2+∠1=90°,
∴∠1=∠5,
∵DE=FE,
在△DEM与△EFA中,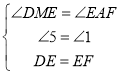 ,
,
∴△DEM≌△EFA,
∴AF=EM,
∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,
∴∠3+∠4=90°,
∴∠3=∠B,
在△DAM与△ABC中, ,
,
∴△DAM≌△ABC,
∴BC=AM,
∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,

∵∠C=90°,
∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,
∴∠2+∠1=90°,∠2=∠B,
在△ADM与△BAC中,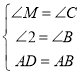 ,
,
∴△ADM≌△BAC,
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠3+∠DEF+∠4=180°,
∴∠3+∠4=90°,
∵∠3+∠5=90°,
∴∠4=∠5,
在△MED与△AFE中, ,
,
∴△MED≌△AFE,
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.

(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某房地产开发公司预计今年![]() 月份将竣工一商品房小区,其中包括高层住宅区和别墅区一共
月份将竣工一商品房小区,其中包括高层住宅区和别墅区一共![]() 万平方米,且高层住宅区的面积不少于别墅区面积的
万平方米,且高层住宅区的面积不少于别墅区面积的![]() 倍.
倍.
(1)别墅区最多多少万平方米?
(2)今年一月初,公司开始出售该小区,其中高层住宅区的销售单价为![]() 元/平方米,别墅区的销售单价为
元/平方米,别墅区的销售单价为![]() 元/平方米,并售出高层住宅区
元/平方米,并售出高层住宅区![]() 万平方米,别墅区
万平方米,别墅区![]() 万平方米,二月时,受最新政策“去库存,满足刚需”以及银行房贷利率打折的影响,该小区高层住宅区的销售单价比一月增加了
万平方米,二月时,受最新政策“去库存,满足刚需”以及银行房贷利率打折的影响,该小区高层住宅区的销售单价比一月增加了![]() ,销售面积比一月增加了
,销售面积比一月增加了![]() ;别墅区的销售单价比一月份减少了
;别墅区的销售单价比一月份减少了![]() ,销售面积比一月增加了
,销售面积比一月增加了![]() ,于是二月份该小区高层住宅区的销售总额比别墅区的销售总额多
,于是二月份该小区高层住宅区的销售总额比别墅区的销售总额多![]() 万元,求
万元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).

上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:

(2)设n条直线把平面最多分成的块数是S,请写出S关于n的表达式.(不需要解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
(1)求两人相遇时李伟离乙地的距离;
(2)请你判断:当张亮返回到甲地时,李伟是否到达乙地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件:
在同一直线上,下面有四个条件:
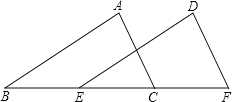
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:____________________________________________;
求证:___________.(注:不能只填序号)
证明如下:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com