
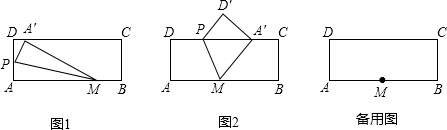
分析 (1)根据折叠的性质得出三角形全等,进而分析AM=A′M=8=2MN,利用含30°角的直角三角形的性质解答即可;
(2)①根据矩形的性质和翻折的性质得出∠A′PM=∠A′MP,再利用等角对等边得出等腰三角形,②根据等腰三角形中边之间的关系得出线段的长度即可;
(3)①根据勾股定理得出t的取值范围;②利用矩形的性质作图进行解答.
解答 解:(1)过点M作MN⊥DC,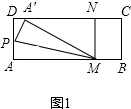
∵四边形ABCD是矩形,
∴MN=BC=4,
∵将△AMP沿着直线MP折叠得到△A′MP,
∴AM=A′M=8=2MN,
∴在Rt△A′MN中,∠MA′C=30°;
(2)①∵A′P与AM是矩形ABCD的对边CD,AB的一部分,
∴A′P∥AM,
∴∠A′PM=∠AMP,
由翻折的性质得:∠AMP=∠A′MP,
∴∠A′PM=∠A′MP,
∴A′P=A′M,
∴△MA′P是等腰三角形;
②∵△MA′P是等腰三角形,
∴PM=AM=A′M=5,A'P=AM=A′M=5,AD=4
∵在RtP A′D′中,根据勾股定理,D′A′=3,由折叠性质得DA=D′A′=3,
∴DP=5-2=3
∴线段DP的长是3cm;
(3)①当点P在AD上,点A′落在DC上时,如图1所示,
过点M作MN⊥DC交DC于点N,
则四边形AMND为矩形,DN=AM=5cm,MN=4cm,
设AP为xcm,则由翻折的性质得:
AM=A′M=5cm,AP=A′P=xcm,
在Rt△A′MN中,A′N=$\sqrt{{5}^{2}-{4}^{2}}=3$cm,
∴DA′=DN-A′N=5-3=2(cm),
在Rt△A′PD中,
A′P2=A′D2+PD2,
即:x2=22+(4-x)2,
解得:x=2.5,
此时t=2.5s;
当点P在DC上,点A′落在DC上时,如图1,
可知DP=3cm,此时,t=7s,
当MA′与DC有交点时,t的取值范围是:2.5≤t≤7,
②当点A′到边AB的距离最大时,
即A′M⊥AB时,t的值为5s,
发现:当点A的落点A′,在以M为圆心,MA为半径的圆上,当圆M与线段CD有唯一交点时,如图2所示,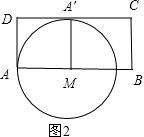
此时AM=4cm,
当圆M交线段CD于点C时,如图3所示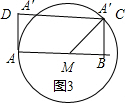
AM=5.8cm,
所以:4<AM≤5.8.
点评 此题考查几何变换问题,用到的知识点是等腰三角形的判定与性质、矩形的性质、勾股定理,关键是利用折叠的前后图形全等进行分析,同时利用矩形的性质和等腰三角形的判定和性质进行解答.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
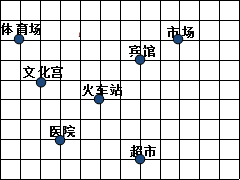 如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.
如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x4+3=0 | B. | $\sqrt{x-2}$=-1 | C. | $\frac{x}{{x}^{2}-1}$=$\frac{1}{{x}^{2}-1}$ | D. | $\sqrt{x+1}$=-x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
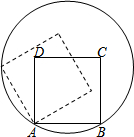 如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.
如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
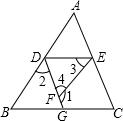 完成下面的证明.
完成下面的证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com