
【题目】![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 上的点,点
上的点,点![]() 是一动点,令
是一动点,令![]() ,
,![]() ,
,![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图①所示,且
上,如图①所示,且![]() ,则
,则![]() _____
_____![]() ;
;
(2)若点![]() 在边
在边![]() 上运动,如图②所示,则
上运动,如图②所示,则![]() 、
、![]() 、
、![]() 之间的关系为______;
之间的关系为______;
(3)如图③,若点![]() 在斜边
在斜边![]() 的延长线上运动
的延长线上运动![]() ,请写出
,请写出![]() 、
、![]() 、
、![]() 之间的关系式,并说明理由.
之间的关系式,并说明理由.

【答案】(1)140°;(2)∠1+∠2=90°+α.(3)如图1,∠2∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠1∠2=∠α90°.
【解析】
(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可.
(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;
(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点,如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,∴∠2∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠2=∠1∠α+∠C,∴∠1∠2=∠α90°.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为8,tan∠C= ![]() ,求线段AB的长,sin∠ADB的值.
,求线段AB的长,sin∠ADB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法回顾:在进行数值估算时,我们常根据所求数值的条件确定它的大致范围,然后通过逐步缩小数值存在范围的方法,最终求得较为准确的数值.
如我们在探究面积为2的正方形的边长a的值时,有如下探究过程:
1<a<2 | 1<s<4 |
1.4<a<1.5 | 1.96<s<2.25 |
1.41<a<1.42 | 1.9881<s<2.0164 |
1.414<a<1.415 | 1.999396<s<2.002225 |
我们也可以借助数轴直观地看出“逐步缩小数值的存在范图”的过程,

这种方法在我们的解决向题的过程中经常会用到
问题提出:a是小于100的正整数,已知它的立方,不借助计算器,如何确定a呢?
问题探究:我们不妨由简单到复杂,从一位整数的立方开始硏究
步骤一、若13<a3<103,则1<a<10.即已知一个一位整数的立方为a3,怎样确定a?
易得:13=1,23=8,33=27,43=64,53=125,63=216,73=343:83=512,93=729,可以通过从1到9的九个整数的立方值确定这个数.观察这九个立方值我们还能发现,他们的个位数字各不相同.
步骤二、若103<a3<1003.则10<a<100,即已知一个两位数的立方为a3,怎样确定a?我们不妨举几个特例,以便寻找解决问题的方法.
特例1.如果一个两位整数a的立方是5832,怎样确定a?
因为103<5832<1003,所以10<a<100,a是一个两位数.
又因为103<5832<203,所以我们可以确定5832的十位数字是 ;再根据步骤一我们就能得出它的个位数是 ;从而确定这个两位数是 .
特例2.如果x是一个两位整数,且x3=614125,请你仿照上面的过程说明你确定这个两位整数的方法.
拓展应用:一颗近似球形的小行星的体积的为2624000πm3,请你根据以上方法求出这个小行星的半径.(球的体积公式v=![]() πR3)
πR3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,两个函数y=x,y=﹣![]() x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复习课中,教师给出关于x的函数y=2kx2-(4k+1)x-k+1(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论,教师作为活动一员,又补充一些结论,并从中选出如下四条:
①存在函数,其图象经过(1,0)点;
②存在函数,该函数的函数值y始终随x的增大而减小;
③函数图象有可能经过两个象限;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中正确的结论有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦AB=(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).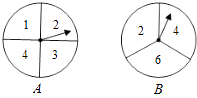
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:记s=x+y.当s<6时,甲获胜,否则乙获胜.你认为这个游戏公平吗?对谁有利?
(3)请你利用两个转盘,设计一个公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com