
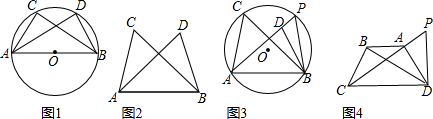
分析 发现:(1)根据不在同一条直线上的三点能够确定一个圆即可得到结论;
思考:(1)根据∠ACB=∠ADB=90°,即可得到结论;
(2)如图①,假设点D在⊙O外,设AD交⊙O于点E,连接BE,根据圆周角定理得到∠AEB=∠ACB,根据外角的性质得到∠AEB>∠D于是得到这个结论与条件中的∠ACB=ADB矛盾,即可得到结论;
应用:由∠CAD=∠CBD=90°,推出A,B,C,D四点在以CD为直径的同一个圆上,根据圆周角定理得到∠ACD=∠ABD,推出∠ACD=∠ADP,由于∠ACD+∠ADC=90°,等量代换得到∠ADC+∠ADP=90°,即可得到结论.
解答  解:发现:(1)若平面上三点能够确定一个圆,那么这三点所满足的条件是三点不在同一条直线上,
解:发现:(1)若平面上三点能够确定一个圆,那么这三点所满足的条件是三点不在同一条直线上,
故答案为:三点不在同一条直线上;
思考:(1)∠ACB=∠ADB=90°,那么点A,B,C,D四点在同一个圆上,
故答案为:在;
(2)如图①,假设点D在⊙O外,设AD交⊙O于点E,连接BE,易得∠AEB=∠ACB,又由∠AEB是△BED的外角,∴∠AEB>∠D,∵∠ACB=∠AEB,∴∠ACB>∠ADB,这个结论与条件中的∠ACB=∠ADB矛盾,∴点D不在圆外,
∴D一定在圆上;
应用:∵∠CAD=∠CBD=90°,
∴A,B,C,D四点在以CD为直径的同一个圆上,
∴∠ACD=∠ABD,
∵∠ABD=∠ADP,
∴∠ACD=∠ADP,
∵∠ACD+∠ADC=90°,
∴∠ADC+∠ADP=90°,
∴∠ADP=90°,
∴DP为Rt△ACD的外接圆的切线.
点评 本题考查的是点与圆的位置关系、圆周角定理以及反证法的应用,掌握反证法的一般步骤、同弧所对的圆周角相等是解题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | am与bm | B. | a2m与b2m | C. | am与-bm | D. | a2m与-b2m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+6=0 | B. | $\frac{2}{3}$x=2 | C. | 5-3x=1 | D. | 3(x-1)=x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×10-5 | B. | 3.5×10-4 | C. | 0.35×10-4 | D. | 3.5×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
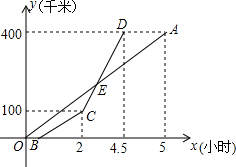 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com