
分析 设甲的速度是x千米/时,乙的速度为y千米/时,根据如果乙先走20km,那么甲用1h就能追上乙;如果乙先走1h,那么甲只用15min就能追上乙列出方程组即可.
解答 解:设甲的速度是x千米/时,乙的速度为y千米/时,
由题意得,$\left\{\begin{array}{l}{x=y+20}\\{\frac{5}{4}y=\frac{1}{4}x}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=y+20}\\{\frac{5}{4}y=\frac{1}{4}x}\end{array}\right.$
点评 本题考查了二元一次方程组的应用,此题是一个行程问题,主要考查的是追及问题,根据路程=速度×时间即可列出方程组.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
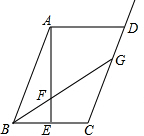 (1)探究一
(1)探究一查看答案和解析>>
科目:初中数学 来源: 题型:解答题
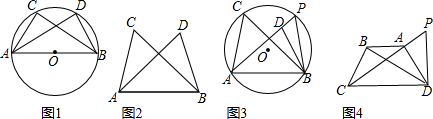
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
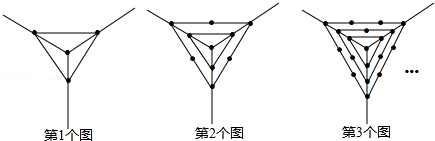
 如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.
如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com