
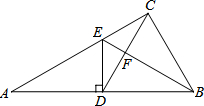
 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F. 证明:(1)∵DE⊥AB,∠ACB=90°,
证明:(1)∵DE⊥AB,∠ACB=90°,
|
|


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
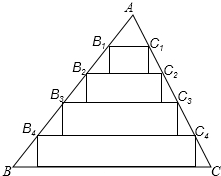 给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.
给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
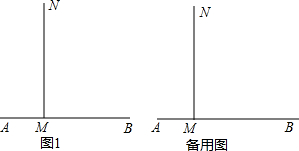 已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.
已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com