练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
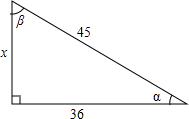
    12．如图，分别求∠α和∠β的正弦、余弦和正切．

    分析 首先利用勾股定理得出x的值，进而利用锐角三角函数关系得出答案．

    解答 解：由题意可得：x=$\sqrt{4{5}^{2}-3{6}^{2}}$=27，
    则sinα=$\frac{27}{45}$=$\frac{3}{5}$，cosα=$\frac{36}{45}$=$\frac{4}{5}$，tanα=$\frac{27}{36}$=$\frac{3}{4}$，
    sinβ=$\frac{36}{45}$=$\frac{4}{5}$，cosβ=$\frac{27}{45}$=$\frac{3}{5}$，tanβ=$\frac{36}{27}$=$\frac{4}{3}$．

    点评 此题主要考查了锐角三角函数关系，正确把握锐角三角函数定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．若a＜0，化简-|-a|．
    解答：因为a＜0  …①
         所以-a＞0  …②
         所以-|-a|=-a  …③
    以上解答过程错在③步，为什么？请给予更正．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）在数轴上，距离原点2个单位长度的点有几个？它们分别表示什么数？
    （2）在数轴上，距离表示数1的点2个单位长度的点有几个？它们分别表示什么数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．若有理数a满足$\root{3}{1-{a}^{2}}=1-{a}^{2}$，$\sqrt{1-\frac{1}{3}b}=0$，求$\root{b}{a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．根据下列条件分别求二次函数的表达式．
    （1）已知二次函数的图象经过点（-2，-1），且当x=-1时，函数有最大值2．
    （2）已知二次函数图象的对称轴是直线x=1，与坐标轴交于点（0，-1），（-1，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．用“＞”或“＜”填空：
    （1）如果a是负数，那么-a＞0；
    （2）如果-a是负数，那么a＞0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．通过估算比较下列每组数的大小：
    （1）$\sqrt{12}$与3.14；
    （2）$\sqrt{3}$-2与$\frac{-\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知|2z-y|+$\sqrt{y-4}$+4x2+4xy+y2=0，求x，y，z．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知方程2x2-5x+k=0的两根互为倒数，求k．

    查看答案和解析>>

    同步练习册答案