
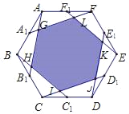
【题目】如图,点A1,B1,C1,D1,E1,F1分别是正六边形ABCDEF六条边的中点,连接AB1,BC1,CD1,DE1,EF1,FA1后得到六边形GHIJKL,则S六边形GHIJKI:S六边形ABCDEF的值为____.
【答案】![]() .
.
【解析】
设正六边形ABCDEF的边长为4a,则AA1=AF1=FF1=2a.求出正六边形的边长,根据S六边形GHIJKI:S六边形ABCDEF=(![]() )2,计算即可;
)2,计算即可;
设正六边形ABCDEF的边长为4a,则AA1=AF1=FF1=2a,
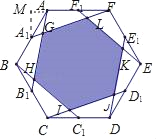
作A1M⊥FA交FA的延长线于M,
在Rt△AMA1中,∵∠MAA1=60°,
∴∠MA1A=30°,
∴AM=![]() AA1=a,
AA1=a,
∴MA1=AA1·cos30°=![]() a,FM=5a,
a,FM=5a,
在Rt△A1FM中,FA1=![]() ,
,
∵∠F1FL=∠AFA1,∠F1LF=∠A1AF=120°,
∴△F1FL∽△A1FA,
∴![]() ,
,
∴![]() ,
,
∴FL=![]() a,F1L=
a,F1L=![]() a,
a,
根据对称性可知:GA1=F1L=![]() a,
a,
∴GL=2![]() a﹣
a﹣![]() a=
a=![]() a,
a,
∴S六边形GHIJKI:S六边形ABCDEF=(![]() )2=
)2=![]() ,
,
故答案为:![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
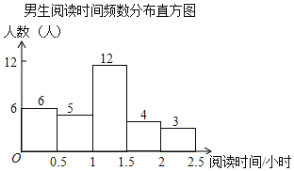
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数![]() 的图象上,边CD在x轴上,点B在y轴上.已知
的图象上,边CD在x轴上,点B在y轴上.已知![]() .
.
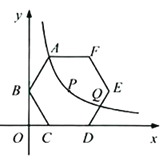
(1)点A是否在该反比例函数的图象上?请说明理由.
(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标.
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李白笔下“孤帆一片日边来”描述了在喷薄而出的红日映衬下,远远望见一叶帆船驶来的壮美河山之境.聪明的小芬同学利用几何图形,构造出了此意境!如图半径为5的⊙0在线段AB上方,且圆心O在线段AB的中垂线上,到AB的距离为![]() ,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=
,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=![]() ,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )
,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以线段AB上的点O为圆心,0B为半径作圆O,分别与边AB,BC相交于D、E两点,过点E作EF⊥AC于F.
(1)判断直线EF与⊙O的位置关系,并说明理由.
(2)若OB=3,cosB=![]() ,求线段BE的长.
,求线段BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数m,当其自变量的值为m时,其函数值等于﹣m,则称﹣m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零.
例如,图中的函数有4,﹣1两个反向值,其反向距离n等于5.
(1)分别判断函数y=﹣x+1,y=![]() ,y=x2有没有反向值?如果有,直接写出其反向距离;
,y=x2有没有反向值?如果有,直接写出其反向距离;
(2)对于函数y=x2﹣b2x,
①若其反向距离为零,求b的值;
②若﹣1≤b≤3,求其反向距离n的取值范围;
(3)若函数y= 请直接写出这个函数的反向距离的所有可能值,并写出相应m的取值范围.
请直接写出这个函数的反向距离的所有可能值,并写出相应m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
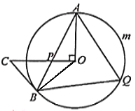
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某校招聘教师一名,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示:
应聘者 | 专业知识 | 讲课 | 答辩 |
甲 | 70 | 85 | 80 |
乙 | 90 | 85 | 75 |
丙 | 80 | 90 | 85 |
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5:4:1.请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
(2)我市举行了某学科实验操作考试,有A、B、C、D四个实验,规定每位学生只参加其中一个实验的考试,并由学生自己抽签决定具体的考试实验.小王,小张,小厉都参加了本次考试.
①小厉参加实验D考试的概率是 ;
②用列表或画树状图的方法求小王、小张抽到同一个实验的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com