
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
分 组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5 16 0.32
90.5~100.5
合 计 50 1.00
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?


【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表;频数(率)分布折线图.
【分析】(1)首先计算出抽取的学生数:用其中一组的频数÷这一组频率得出总数,进而得出各组的学生数以及频率;
(2)根据(1)中所求数据,即可补全频率分布直方图;
(3)利用(2)中条形图或频率分布表可得出,全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(4)若成绩在90分以上(含90分)为优秀,则这随机抽取的50个人中优秀的频率为0.24,进而得出850名学生中优秀人数.
【解答】解:(1)抽取的学生数:4÷0.08=50,
60.5~70.5的学生数为:50×0.16=8,
90.5~100.5的学生数:50﹣4﹣8﹣10﹣16=12,
频率=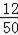
 =0.24;
=0.24;
分组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 8 0.16
70.5~80.5 10 0.20
80.5~90.5 16 0.32
90.5~100 12 0.24
合计 50 1.00
(2)如图所示:
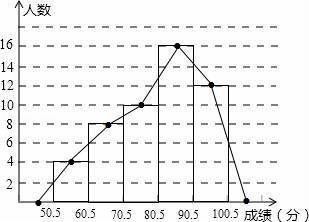

(3)利用(2)中条形图或频率分布表可得出,全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多.
(4)∵随机抽取的50个人中优秀的频率为0.24,
∴850名学生中优秀人数为:850×0.24=204(人),
答:该校成绩优秀的约为204人.
故答案为:80.5~90.5.
【点评】本题考查了读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
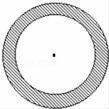
如图是在地上画出的半径分别为2m和3m的同心圆.现在你和另一人分别蒙上眼睛,并在一定距离外向圈内掷一粒较小的石子,规定一人掷中小圆内得胜,另一人掷中阴影部分得胜,未掷入半径为3m的圆内或石子压在圆周上都不算.
(1)你会选择掷中小圆内得胜,还是掷中阴影部分得胜?为什么?
(2)你认为这个游戏公平吗?如果不公平,那么大圆不变,小圆半径是多少时,使得仍按原规则进行,游戏是公平的?(只需写出小圆半径,不必说明原因)

查看答案和解析>>
科目:初中数学 来源: 题型:
在直角坐标系中,一条直线经过A(﹣1,5),P(﹣2,a),B(3,﹣3)三点.
(1)求a的值;
(2)设这条直线与y轴相交于点D,求△OPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
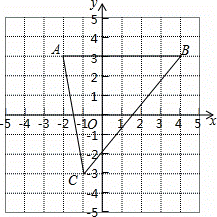
如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com