
【题目】[阅读理解]射线![]() 是
是![]() 内部的一条射线,若
内部的一条射线,若![]() 则我们称射线
则我们称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
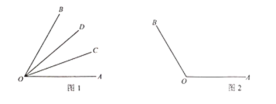
例如,如图1,![]() ,则
,则![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线:同时,由于
的伴随线:同时,由于![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
[知识运用]
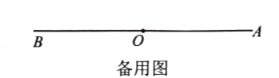
(1)如图2,![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,则
的伴随线,则![]() ,若
,若![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,则
的平分线,则![]() 的度数是 .(用含
的度数是 .(用含![]() 的代数式表示)
的代数式表示)
(2)如图,如![]() ,射线
,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,射线
的速度逆时针旋转,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线![]() 与射线
与射线![]() 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.

①是否存在某个时刻![]() (秒),使得
(秒),使得![]() 的度数是
的度数是![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②当![]() 为多少秒时,射线
为多少秒时,射线![]() 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线.
【答案】(1)![]() ,
,![]() ;(2)①存在,当
;(2)①存在,当![]() 秒或25秒时,∠COD的度数是20
秒或25秒时,∠COD的度数是20![]() ;②当
;②当![]() ,
,![]() ,
,![]() ,
,![]() 时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
【解析】
(1)根据伴随线定义即可求解;
(2)①利用分类讨论思想,分相遇之前和之后进行列式计算即可;
②利用分类讨论思想,分相遇之前和之后四个图形进行计算即可.
(1)∵![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,
的伴随线,
根据题意,![]() ,则
,则![]() ;
;
∵![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)射线OD与OA重合时,![]() (秒),
(秒),
①当∠COD的度数是20°时,有两种可能:
若在相遇之前,则![]() ,
,
∴![]() ;
;
若在相遇之后,则![]() ,
,
∴![]() ;
;
所以,综上所述,当![]() 秒或25秒时,∠COD的度数是20°;
秒或25秒时,∠COD的度数是20°;
②相遇之前:
(i)如图1,

OC是OA的伴随线时,则![]() ,
,
即![]() ,
,
∴![]() ;
;
(ii)如图2,
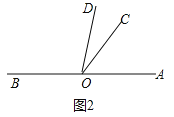
OC是OD的伴随线时,
则![]() ,
,
即![]() ,
,
∴![]() ;
;
相遇之后:
(iii)如图3,
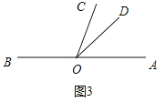
OD是OC的伴随线时,
则![]() ,
,
即![]() ,
,
∴![]() ;
;
(iv)如图4,

OD是OA的伴随线时,则![]() ,
,
即![]() ,
,
∴![]() ;
;
所以,综上所述,当![]() ,
,![]() ,
,![]() ,
,![]() 时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.
时,OC、OD、OA中恰好有一条射线是其余两条射线的伴随线.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
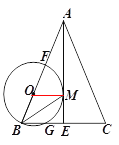
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2 
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
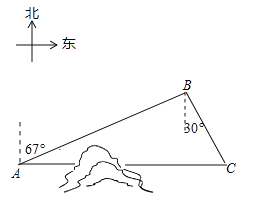
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
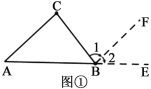
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
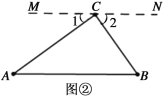
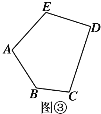
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式![]() 的解集(满足不等式的所有解).
的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出![]() 恰好是3时
恰好是3时![]() 的值,并在数轴上表示为点
的值,并在数轴上表示为点![]() ,
,![]() ,如图所示.观察数轴发现,
,如图所示.观察数轴发现,
![]()
以点![]() ,
,![]() 为分界点把数轴分为三部分:
为分界点把数轴分为三部分:
点![]() 左边的点表示的数的绝对值大于3;
左边的点表示的数的绝对值大于3;
点![]() ,
,![]() 之间的点表示的数的绝对值小于3;
之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①![]() 的解集是 ;
的解集是 ;
②![]() 的解集是 .
的解集是 .
(2)求绝对值不等式![]() 的解集.
的解集.
(3)直接写出不等式![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
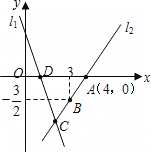
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com