【题目】已知正比例函数
和反比例函数
，
与
和
的部分对应值如下表所示：
| … |
| 4 | 8 | … |
| … | 1 |
| 4 | … |
| … | 4 | 2 |
| … |
（1）求
、
、
的值；
（2）指出当
时，正比例函数图像与反比例函数图像的交点坐标；
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发，用t秒表示移动的时间(0≤t≤6)那么:
(1)当t为何值时，△QAP为等腰直角三角形？
(2)对四边形QAPC的面积，提出一个与计算结果有关的结论；
(3)当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．
（1）求证：∠DAC=∠DBA；
（2）求证：PD=PF；
（3）连接CD，若CD﹦3，BD﹦4，求⊙O的半径和DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平面直角坐标系中，点
坐标为
，点
是
轴正半轴上一点，且
，点
是
轴上位于点右侧的一个动点，设点的坐标为
．
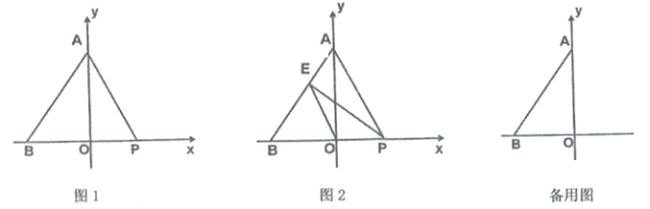
（1）点的坐标为（ ）；
（2）当
是等腰三角形时，求点的坐标；
（3）如图2，过点作
交线段
于点
，连接
，若点关于直线的对称点为
，当点恰好落在直线
上时，
．（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，正方形ABCD中，E、F分别是BC、DC上的一点，连接AE、AF， AE、AF交于点H且∠AHB=90°.
（1）求证：BE=CF．
（2）若正方形面积是25m2，BE=
AD，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是
，则矩形ABCD的面积是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，山顶建有一座铁塔，塔高BC=80米，测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°，塔顶C点的仰角为60°．已测得小山坡的坡角为30°，坡长MP=40米．求山的高度AB（精确到1米）．（参考数据：
≈1.414，
≈1.732）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，ΔP1OA1，ΔP2A1A2是等腰直角三角形，点P1、P2在函数y=
(x>0)的图象上，斜边OA1、A1A2都在x轴上，则点A2的坐标是____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道：x2﹣6x＝(x2﹣6x+9)﹣9＝(x﹣3)2﹣9；﹣x2+10＝﹣(x2﹣10x+25)+25＝﹣(x﹣5)2+25，这一种方法称为配方法，利用配方法请解以下各题：
(1)按上面材料提示的方法填空：a2﹣4a＝ ＝ ．﹣a2+12a＝ ＝ ．
(2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．
(3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
