【题目】如图，已知AB∥CD,∠EAF =
∠EAB,∠ECF=∠ECD ,∠AFC=62°,则∠AEC度数是________
【答案】93°
【解析】
连接AC，设∠EAF=x°，∠ECF=y°，则∠EAB=3x°，∠ECD=3y°，可得∠BAF=2x°，∠DCF=2y°，由AB∥CD，三角形的内角和定理，可得∠AFC=2（x°+y°）=62°，计算得到x°+y°=31°，则∠AEC=3（x°+y°），即可得到答案.
解，如图，连接AC，设∠EAF=x°，∠ECF=y°，
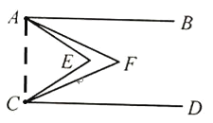
∴∠EAB=3x°，∠ECD=3y°，
∴∠BAF=2x°，∠DCF=2y°，
∵AB∥CD，
∴∠BAC+∠ACD=180°，
∴∠BAF+∠FAC+∠ACF+∠DCF=180°，
∵∠FAC+∠ACF+∠AFC=180°，
∴∠AFC=∠BAF+∠DCF=2（x°+y°）=62°，
∴x°+y°=31°.
同理可求：∠AEC=∠BCE+∠DCE=3（x°+y°），
∴∠AEC=
.
故答案为：93°.
目标测试系列答案科目：初中数学 来源： 题型：
【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．
请结合以上信息解答下列问题：
（1）m= ；
（2）请补全上面的条形统计图；
（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为 ；
（4）已知该校共有1200名学生，请你估计该校约有 名学生最喜爱足球活动．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）+5，-3，+10，-8，-6，+12，-10
（1）守门员最后是否回到了球门线的位置？
（2）在练习过程中，守门员离开球门最远距离是多少米？
（3）守门员全部练习结束后，他共跑了多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题，求
的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗？请按照下面的问题试一试：
（1）由
,确定的立方根是 位数；
（2）由的个位数是
确定的立方根的个位数是 ；
（3）如果划去后面的三位
得到数
,而
,由此能确定的立方根的十位数是 ；所以的立方根是 ；
（4）用类似的方法，请说出
的立方根是 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标
中，已知三点A(1，3)，B(3，3)，C(3，1)，反比例函数
的图象经过其中的两点，另外一点在直线
上．
（1）填空： 
＝________， 
＝________；
（2）请你求出直线
与反比例函数
的图象的交点坐标；
（3）当
时，请直接写出相应的
的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数轴上A，B，C三个点对应的数分别为a，b，x，且A，B到﹣1所对应的点的距离都等于7，点B在点A的右侧，
（1）请在数轴上表示点A，B位置，a= ，b= ；
（2）请用含x的代数式表示CB= ；
（3）若点C在点B的左侧，且CB=8，点A以每秒2个单位长度的速度沿数轴向右运动，当AC=2AB且点A在B的左侧时，求点A移动的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
