练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，过正五边形ABCDE的顶点D作直线l∥AB，则∠1的度数是36°．

    分析 根据正五边形的性质求出∠DCB=∠ABC=$\frac{1}{5}$×（5-2）×180°=108°，求出∠OCB=∠OBC=72°，根据三角形内角和定理求出∠O，根据平行线的性质得出∠1=∠O，代入求出即可．

    解答 解：
    延长DC、AB交于O，
    ∵五边形ABCDE是正五边形，
    ∴∠DCB=∠ABC=$\frac{1}{5}$×（5-2）×180°=108°，
    ∴∠OCB=∠OBC=180°-108°=72°，
    ∴∠O=180°-72°-72°=36°，
    ∵直线l∥AB，
    ∴∠1=∠O=36°，
    故答案为：36°．

    点评 本题考查了多边形和平行线的性质的应用，能正确作出辅助线是解此题的关键，注意：两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．已知抛物线L：y=ax2+bx+c（a≠0），经过A（3，0），B（-1，0），C（0，3）三点．
    （1）求这条抛物线的表达式；
    （2）求该抛物线顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查，随机抽取了若干名学生进行调查，并制作统计图，据此统计图估计该校八年级支持“分组合作学习”方式的学生（含非常喜欢和喜欢两种情况）约为（　　）
    A．180名B．210名C．240名D．270名

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各数中，不是无理数的是（　　）
    A．$\sqrt{5}$B．-3.14C．$\root{3}{36}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

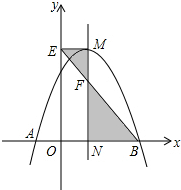    13．如图，抛物线y=ax2+2x+c与x轴交于A，B两点，它的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连接BE交MN于点F，已知点A的坐标为（-1，0），B的坐标为（3，0）．
    （1）求该抛物线的解析式及顶点M的坐标；
    （2）直接写出△EMF与△BNF的面积之比以及点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．观察中国象棋的棋盘，其中“马”的位置可以用一个数对（3，5）来表示，则表示“兵”点位置的数对是（6，7）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．对于两个不相等的有理数a，b，我们规定符号Max{a，b}表示a，b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{-$\frac{1}{x}$，$\frac{1}{x}$}=$\frac{2}{3-x}$的解为x=1或x=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．设四位数＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞abcd?$\overline{abcd}$满足10d3=1000a+100c+10d+b，则这样的四位数有3个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知正五边形的边长是48cm，求它的半径R5和边心距r5．（精确到0.1cm，已知sin36°≈0.5878．）

    查看答案和解析>>

    同步练习册答案